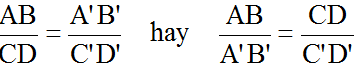Phát biểu định lý Ta-lét trong hình học phẳng.

Những câu hỏi liên quan
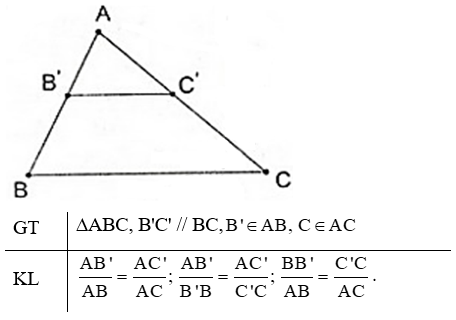
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét trong tam giác ?
Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Đúng 1
Bình luận (0)
Phát biểu định lí Ta – lét trong không gian.
Định lí Ta – lét trong không gian:
- Định lí thuận (Định lí Ta – lét)
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ, nghĩa là:
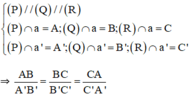
Định lí đảo (Định lí Ta – lét đảo)
Giả sử trên hai đường thẳng a và a' lần lượt lấy hai bộ ba điểm (A, B, C) và (A', B', C') sao cho AB/A'B'= BC/B'C' = CA/C'A'
Khi đó ba đường thẳng AA', BB', CC' cùng song song với một mặt phẳng, nghĩa là ba đường thẳng đó nằm trên ba mặt phẳng song song với nhau.
Đúng 0
Bình luận (0)
Phát biểu định lí Ta - lét trong không gian ?
Ba mặt phẳng đôi một song song chắn ra trên hai cát tuyến bất kì hai đoạn thẳng tỉ lệ .
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Ta - lét đảo ?
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đúng 0
Bình luận (0)
gt: DE giao AB={ D}, DE giao ={ E}
\(\frac{AD}{AB}\)= \(\frac{AE}{AC}\)
kl: =) DE// BC
Đúng 0
Bình luận (0)
Định lý Ta - lét đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Vẽ hình và Giả thuyết, Kết luận:

GT: △ABC,\(\frac{AM}{AB}=\frac{AN}{AC},\frac{MB}{AB}=\frac{NC}{AC},\frac{AM}{MB}=\frac{AN}{NC}\)
KL: MN // BC
Đúng 0
Bình luận (0)
Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Ta - lét ?
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:
Đúng 0
Bình luận (0)
Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.
Đúng 0
Bình luận (0)
Nhắc lại định lý Ta-lét trong tam giác.
Chưng minh định lý Ta - lét
Tam giác ABC có MN // BC (M thuộc AB, N thuộc AC)
S(ACM)/S(ABC) = AM/AB (1)
S(ABN)/S(ABC) = AN/AC (2)
Mà S(ACM) = S(AMN) + S(CMN) (3)
và S(ABN) = S(AMN) + SBMN) (4)
Mặt khác do MNCB hình thang nên dễ dàng chứng minh
S(CMN) = S(BMN) (5)
Từ (3) , (4) và (5) cho:
S(ACM) = S(ABN) (6)
(1) , (2) và (6) cho:
AM/AB = AN/AC (đpcm)
-----------
Cách viết S(ABC) đọc là diện tích tam giác ABC
Đúng 0
Bình luận (0)
Giả sử tam giác ABC và DE // BC
Ta cần C/M \(\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}\)
Vì DE // BC
=> ^B = ^D1 ( đồng vị )
Xét tam giác ABC và tam giác ADE có :
\(\widehat{A}\)chung
\(\widehat{B}=\widehat{D_1}\)(CMT)
\(\Rightarrow\Delta ABC~\Delta ADE\left(g.g\right)\)(~ là đồng dạng nhé )
\(\Rightarrow\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}\)( Đpcm )
Vậy ...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho mình hỏi cách chứng minh định lý ta lét?
Cách chứng minh định lý ta lét : v
Đúng 0
Bình luận (0)
Bạn nào có định nghĩa với chuyên đề về định lý Ta-lét ''mở rộng'' thì cho mình xin nhé =v
Bạn tham khảo thêm tại đây :
Lý thuyết định lí ta-lét. định lí đảo và hệ quả của định lí ta-lét toán 8
Đúng 0
Bình luận (0)