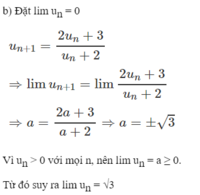Biết rằng dãy số ( u n ) có giới hạn là 0. Giải thích vì sao dãy số ( v n ) với v n = | u n | cũng có giới hạn là 0. Chiều ngược lại có đúng không?

Những câu hỏi liên quan
Biết rằng dãy số \(\left(u_n\right)\) có giới hạn là 0. Giải thích vì sao dãy số \(\left(v_n\right)\) với \(v_n=\left|u_n\right|\) cũng có giới hạn là 0. Chiều ngược lại có đúng không ?
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Vì sao dãy số \(\left(u_n\right)\) với \(u_n=\left(-1\right)^n\) không thể có giới hạn là 0 khi \(n\rightarrow+\infty\) ?
Cho hai dãy số
u
n
và
v
n
. Biết
|
u
n
–
2
|
≤
v
n
với mọi n và
l
i
m
v
n
0
. Có kết luận gì về giới hạn...
Đọc tiếp
Cho hai dãy số u n và v n . Biết | u n – 2 | ≤ v n với mọi n và l i m v n = 0 . Có kết luận gì về giới hạn của dãy số u n ?
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
Đúng 0
Bình luận (0)
Cho biết dãy số
(
u
n
)
có giới hạn hữu hạn, còn dãy số
(
v
n
)
không có giới hạn hữu hạn. Dãy số
(
u
n
+
v
n
)
có thể có giới hạn hữu hạn không?
Đọc tiếp
Cho biết dãy số ( u n ) có giới hạn hữu hạn, còn dãy số ( v n ) không có giới hạn hữu hạn. Dãy số ( u n + v n ) có thể có giới hạn hữu hạn không?
Dãy ( u n + v n ) không có giới hạn hữu hạn.
Thật vậy, giả sử ngược lại ( u n + v n ) có giới hạn hữu hạn.
Khi đó, các dãy số ( u n + v n ) v à ( u n ) cùng có giới hạn hữu hạn, nên hiệu của chúng cũng là một dãy có giới hạn hữu hạn, nghĩa là dãy số có số hạng tổng quát là u n + v n − u n = v n có giới hạn hữu hạn. Điều này trái với giả thiết ( v n ) không có giới hạn hữu hạn.
Đúng 0
Bình luận (0)
Cho dãy số thực (un) xác định bởi \(\left\{{}\begin{matrix}u_1=2019\\u^2_n+2018u_n-2020u_{n+1}+1=0\left(n\in N\cdot\right)\end{matrix}\right.\). Tìm giới hạn của dãy số (Sn), biết: Sn = \(\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)
Đúng 1
Bình luận (0)
Tính \(\lim\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{16}+...+\dfrac{1}{n^2}\right)\).
Chỉ giải bằng những kiến thức có trong bài "Bài 1: Giới hạn của dãy số". Giải thích chi tiết bước làm và tại sao lại làm như vậy.