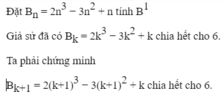Chứng minh rằng với mọi n ∈ N ∗ ta có 11 n + 1 + 12 2 n − 1 chia hết cho 133.

Những câu hỏi liên quan
chứng minh rằng với mọi n thuộc N ta có 3^2^4n+1 + 2 cia hết cho 11
Chứng minh rằng với mọi n thuộc N*, ta có
Đọc tiếp
Chứng minh rằng với mọi n thuộc N*, ta có
a.
Với \(n=1\Rightarrow4\ge3+1\) (đúng)
Giả sử đẳng thức đúng với \(n=k\ge1\) hay \(4^k\ge3k+1\)
Ta cần chứng minh nó cũng đúng với n=k+1 hay: \(4^{k+1}\ge3\left(k+1\right)+1\)
Thật vậy, ta có:
\(4^{k+1}=4.4^k\ge4\left(3k+1\right)=12k+4=3\left(k+1\right)+1+9k>3\left(k+1\right)+1\) (đpcm)
b.
Với \(n=1\Rightarrow\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}>1\) (đúng)
Giả sử BĐT đúng với \(n=k\) hay: \(\dfrac{1}{k+1}+\dfrac{1}{k+2}+...+\dfrac{1}{3k+1}>1\)
\(\Rightarrow\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3k+1}>1-\dfrac{1}{k+1}\)
Ta cần chứng minh nó cũng đúng với n=k+1 hay:
\(\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3\left(k+1\right)+1}>1\)
\(\Leftrightarrow\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3k+4}>1\)
Thật vạy, ta có:
\(\dfrac{1}{k+2}+\dfrac{1}{k+3}+..+\dfrac{1}{3k+4}\)
\(=\dfrac{1}{k+2}+...+\dfrac{1}{3k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}\)
\(>1-\dfrac{1}{k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}\) (1)
Mặt khác ta có:
\(\dfrac{1}{3k+2}+\dfrac{1}{3k+4}-\dfrac{2}{3k+3}=\dfrac{2}{\left(3k+2\right)\left(3k+3\right)\left(3k+4\right)}>0\)
\(\Rightarrow\dfrac{1}{3k+2}+\dfrac{1}{3k+4}>\dfrac{2}{3k+3}\)
\(\Rightarrow\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}>\dfrac{3}{3k+3}=\dfrac{1}{k+1}\) (2)
(1);(2) \(\Rightarrow1-\dfrac{1}{k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}>1\) (đpcm)
Đúng 2
Bình luận (0)
Chứng minh rằng với mọi n ∈ N ∗ ta có 2 n 3 − 3 n 2 + n chia hết cho 6
Chứng minh rằng với mọi số nguyên dương n ≥ 4 ta có: 3\(^{n-1}\) > n(n+2)
- Với \(n=4\Rightarrow3^3>4.6\) (đúng)
- Giả sử BĐT đã cho đúng với \(n=k\ge4\) hay \(3^{k-1}>k\left(k+2\right)\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay: \(3^k>\left(k+1\right)\left(k+3\right)\)
Thật vậy, do \(k\ge4\Rightarrow k-3>0\), ta có:
\(3^k=3.3^{k-1}>3k\left(k+2\right)=3k^2+6k=\left(k^2+4k+3\right)+\left(2k^2+2k-3\right)\)
\(=\left(k+1\right)\left(k+3\right)+2k^2+k+\left(k-3\right)>\left(k+1\right)\left(k+3\right)\) (đpcm)
Đúng 2
Bình luận (0)
Chứng minh rằng với mọi số tự nhiên n ta có:
\(3^{2^{4n+1}}+2⋮11\)
Chứng minh rằng với mọi số tự nhiên n ta có
\(\left(2^{2^{4n+7}}+7\right)⋮11\)
Chứng minh rằng với mọi n >1 ta có: (n!+1; (n+1)!+1) =1
Chứng minh rằng 111...11 (có n ch/s 1) -n chia hết cho 9,với mọi n thuộc N
chứng minh rằng với mọi n ta có n^5/5 +n^3/3+7n/15 thuộc Z
ko hỉu viết lại đề bài đi như thế này à ?
chứng minh rằng với mọi n ta có n5/5 + n5: 3+7n/15 thuộc Z
Đúng 0
Bình luận (0)
2) P = n^5/5 + n^3/3 + 7n/15 =
= (n^5 - n + n)/5 + (n^3 -n +n)/3 + 7n/15
= (n^5 -n)/5 + (n^3 -n)/3 + n/5 + n/3 + 7n/15
* từ câu d ta có n^5 - n chia hết cho 30 => n^5 -n chia hết cho 5
=> (n^5 - n)/5 = a (thuộc Z)
* n^3 - n = n(n²-1)(n²+1) = (n-1)n(n+1)(n²+1) có tích của 3 số nguyên liên tiếp nên chia hết cho 3
=> (n^3 - n)/3 = b (thuộc Z)
* n/5 + n/3 + 7n/15 = 15n/15 = n (thuộc Z)
Vậy: P = a + b + n thuộc Z
Đúng 0
Bình luận (0)
chứng minh rằng với mọi n ta có n^5/5 +n^3/3+7n/15 thuộc Z
chứng minh rằng với mọi n ta có n^5/5 +n^3/3+7n/15 thuộc Z