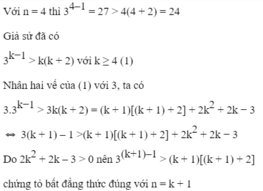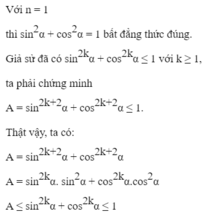Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 1 2 + 3 2 + 5 2 + . . . + 2 n - 1 2 = n 4 n 2 - 1 3

Những câu hỏi liên quan
Chứng minh bất đẳng thức sau
\(\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{n!}< 2\)
Ta có: \(4!>4.3\) ; \(5!>5.4\) ;....; \(n!>n\left(n-1\right)\)
\(\Rightarrow VT=\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...+\frac{1}{n!}< 1+\frac{1}{2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n\left(n-1\right)}\)
\(VT< 1+\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n-1}-\frac{1}{n}\)
\(VT< 2-\frac{1}{n}< 2\) (đpcm)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh đẳng thức sau (
v
ớ
i
n
∈
N
∗
)
2
+
5
+
8
+
.
.
.
+
(
3
n
-
1
)
3
3...
Đọc tiếp
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 2 + 5 + 8 + . . . + ( 3 n - 1 ) = 3 3 n + 1 2
Đặt vế trái bằng S n . Kiểm tra với n = 1 hệ thức đúng.
Giả sử đã có 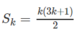 với k ≥ 1.
với k ≥ 1.
Ta phải chứng minh 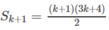
Thật vậy
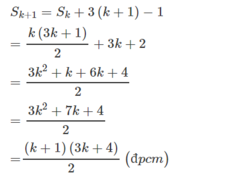
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Với n = 1 thì 2 1 + 2 = 8 > 7 = 2 . 1 + 5
Giả sử bất đẳng thức đúng với n = k ≥ 1 tức là 2k + 2 > 2k + 5 (1)
Ta phải chứng minh nó cũng đúng với n = k + 1,
tức là 2k + 3 > 2(k + 1) + 5 hay 2k + 3 > 2k + 7(2)
Thật vậy, nhân hai vế của (1) với 2, ta được
2k + 3 > 4k + 10 = 2k + 7 + 2k + 3
Vì 2k + 3 > 0 nên 2k + 3 > 2k + 7(đpcm)
Đúng 0
Bình luận (0)
Help
Chứng minh rằng với mọi số nguyên n≥2n≥2, ta luôn có đẳng thức sau :
(1−14)(1−19)...(1−1n2)=n+12n
Chứng minh rằng biểu thức sau không phụ thuộc vào biến: A= 3 (2x-5y)+(3x-y) (-2x) - 1/2 (2-26xy)
Các bạn giúp mình i, mình đang cần gấp ớ <3!!Ta có:
Sửa đề \(A=3\left(2x-5xy\right)+\left(3x-y\right)\left(-2x\right)-\dfrac{1}{2}\left(2-26xy\right)\)
\(A=6x-15xy-6x+2xy-1+13xy\)
\(A=-1\)
Vậy biểu thức sau không phụ thuộc vào biến x
Đúng 0
Bình luận (0)
Cho mình xin Bài tập liên quan tới chủ đề :1.Quan hệ đường kính và dây cung
2.Chứng minh tứ giác nội tiếp giải bài toán liên quan vận dụng kiến thức 2 tam giác đồng dạng để chứng minh đẳng thức tích
3.Các góc trong đường tròn chứng minh song song
Cho các số a, b, c, d > 0 và các bất đẳng thức sau :
(1) 5ad(1 - b2) > 1 (2) 32bc(1 - c2) > 5
(3) 4ac(1 - d2) > 7 (4) 14bd(1 - a2) > 1
Chứng minh rằng trong các bất đẳng thức trên luôn có ít nhất một bất đẳng thức sai.
với n>0 chứng minh bất đẳng thức sau
\(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \frac{1}{2\sqrt{n}}\)
\(\frac{1}{2\sqrt{n+1}}=\frac{1}{\sqrt{n+1}+\sqrt{n+1}}< \frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{\sqrt{n+1}-\sqrt{n}}{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}=\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}=\sqrt{n+1}-\sqrt{n}\)
=> \(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}\)(1)
\(\frac{1}{2\sqrt{n}}=\frac{1}{\sqrt{n}+\sqrt{n}}>\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{\sqrt{n+1}-\sqrt{n}}{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}=\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}=\sqrt{n+1}-\sqrt{n}\)=> \(\frac{1}{2\sqrt{n}}>\sqrt{n+1}-\sqrt{n}\)(2)
Từ (1) và (2) => \(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \frac{1}{2\sqrt{n}}\)
Đúng 0
Bình luận (0)