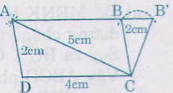
Dựng hình thang ABCD (AB // CD), biết ba cạnh: AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm.

Những câu hỏi liên quan
1. Dựng hình thang cân ABCD (AB//CD) biết AB=1cm, CD=3cm và AD=2cm
2. Dựng hình thang cân ABCD, biết đáy CD=4cm, cạnh bên AD=2cm, đường chéo BD=3cm
1. Dựng hình thang cân ABCD (AB//CD) biết AB1cm, CD3cm và AD2cm2. Dựng hình thang cân ABCD, biết đáy CD4cm, cạnh bên AD2cm, đường chéo BD3cm
Đọc tiếp
1. Dựng hình thang cân ABCD (AB//CD) biết AB=1cm, CD=3cm và AD=2cm
2. Dựng hình thang cân ABCD, biết đáy CD=4cm, cạnh bên AD=2cm, đường chéo BD=3cm
Dựng hình thang ABCD ( AB//CD), biết ba cạnh : AD=2cm, CD=4cm, BC=3cm và đường chéo AC=5cm
Dựng hình thang ABCD (AB//CD), biết ba cạnh : AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm
Dựng đoạn thẳng CD = 4cm.
- Dựng hai đường tròn (C, 5cm) và (D, 2cm) cắt nhau tại A.
- Dựng đường tròn (C, 2cm) và đường tròn (A, 4cm) cắt nhau tại B.
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B' (ngoài điểm B đã kể ở trên)
Các tứ giác ABCD và AB'CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B thuộc đường tròn (A, 4cm) nên AB = 4cm.
ΔABC = ΔDCA (AB = CD = 4cm, AD = BC = 2cm, AC chung) do đó góc BAC = góc DCA là cặp so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4cm, BC = 2cm là hình thang thỏa mãn yêu cầu, AB'CD cũng là hình thang thỏa mãn yêu cầu vì AB' // CD, AD = 2cm, CD = 4cm, CB' = 2cm.
Đúng 0
Bình luận (0)
Dựng hình thang ABCD (AB//CD) biết AD=3cm,BC=4cm,AC=5cm,CD=6cm
Dựng hình thang ABCD, biết hai đáy AB = lcm, CD = 4cm, hai cạnh bên AD = 2cm, BC = 3cm.
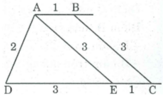
Phân tích:
Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Qua A kẻ đường thẳng song song với BC cắt CD tại E ta thấy tam giác AED xác định vì biết ba cạnh, ta cần xác định đình B và C.
- Đỉnh C nằm trên tia DE, cách D một khoảng bằng 4cm.
- Đỉnh B nằm trên đường thẳng đi qua A song song với đường thẳng DE và cách A một khoảng bằng lcm.
Cách dựng:
- Dựng ∆ ADE biết AD = 2cm, DE = 3cm, AE = 3cm
- Trên tia DE dựng điểm C sao cho DC = 4cm
- Dựng đường thẳng đi qua A và song song với DC, lấy điểm B sao cho AB = lcm. Nối BC ta có hình thang ABCD cần dựng.
Chứng minh:
Thật vậy, theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang.
Ta có: AD = 2cm, DC = 4cm, AB= lcm, hình thang ABCE có hai cạnh đáy AB = EC = 1cm nên BC = AE = 3cm.
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADB luôn dựng được nên hình thang ABCD dựng được, bài toán có một nghiệm hình.
Đúng 0
Bình luận (0)
Dựng hình thang ABCD, biết hai đáy AB = 1cm, CD = 4cm, hai cạnh bên AD = 2cm, BC = 3cm ?
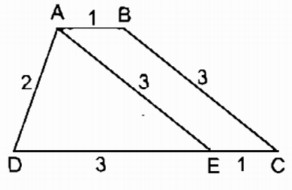
hân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Qua A kẻ đường thẳng song song với BC cắt CD tại E ta thấy tam giác AED xác định vì biết ba cạnh, ta cần xác định đỉnh B và C
– Đỉnh C nằm trên tia DE, cách D một khoảng bẳng 4cm
– Đỉnh B nằm trên đường thẳng đi qua A song song với đường thẳng DE và cách A một khoảng bằng 1cm.
Cách dựng:
QUẢNG CÁO
– Dựng ∆ ADE biết AD = 2cm, DE = 3cm, AE = 3cm
– Trên tia DE dựng điểm C sao cho DC = 4cm
– Dựng đường thẳng đi qua A và song song với DC, lấy điểm B sao cho AB = 1cm. Nối BC ta có hình thang ABCD cần dựng
Chứng minh: Thật vậy theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang.
Ta có: AD = 2cm, DC = 4cm, AB = 1cm, hình thang ABCE có hai cạnh đáy AB = EC = 1cm nên BC = AE = 3cm.
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADE luôn dựng được nên hình thang ABCD dựng được, bài toán có một nghiệm hình.
Đúng 0
Bình luận (0)
Dựng hình thang ABCD (AB//CD) Biết AB = 2cm; AC = 5cm; BD = 3cm và AOB = 120o (với O giao điểm hai đường chéo).
/Làm đủ 4 bước dựng hình\
Dựng hình thang ABCD (AB // CD), biết \(\widehat{D}=90^0;AD=2cm;CD=4cm,BC=3cm\)