Khảo sát và vẽ đồ thị các hàm số
a) y = 2 - 3x - x 2 ;
b) x 3 - x 2 + x;
c) y = - x 4 + 2 x 3 + 3.
Những câu hỏi liên quan
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Khảo sát sự biến thiên và vẽ đồ thị hàm số Y=-x^3+3x^2-4x+2
a) khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2+3\)
b) vẽ đồ thị hàm số \(y=\left|x^4-2x^2+3\right|\)
Khảo sát và vẽ đồ thị hàm số Y=-3x +3x²+1
\(y=3x^2-3x+1\)
=>\(y'=3\cdot2x-3=6x-3\)
Hàm số \(y=3x^2-3x+1\) đồng biến khi 6x-3>0
=>x>1/2
Hàm số y=3x2-3x+1 nghịch biến khi 6x-3<0
=>x<1/2
vẽ đồ thị:
Đúng 0
Bình luận (0)
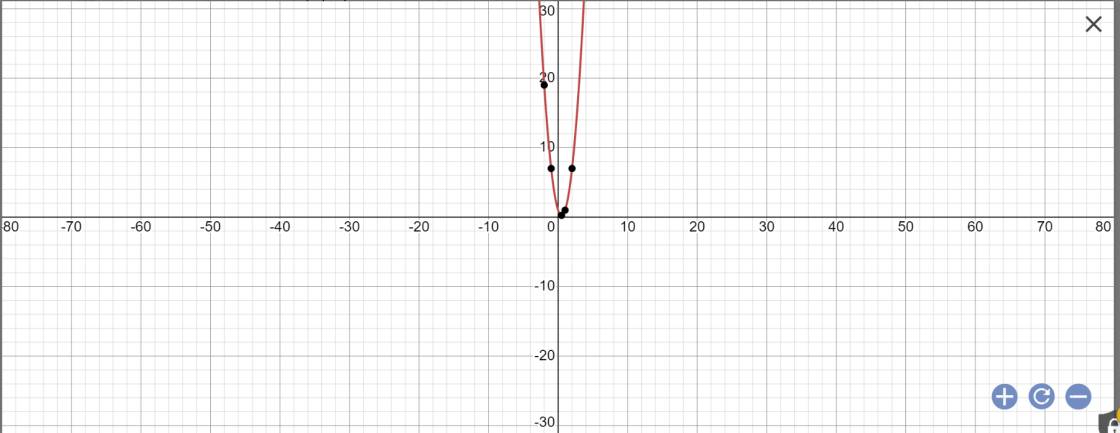
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = x + 3 x + 1
Khảo sát hàm số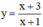 
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên:
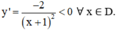
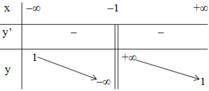
⇒ Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
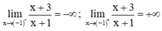
⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.
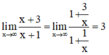
⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
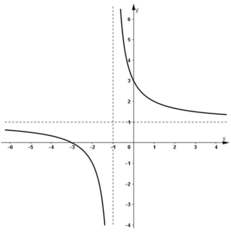
- Đồ thị:
+ Giao với Ox: (-3; 0)
+ Giao với Oy: (0; 3)
+ Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:a. yx3-3x+2b. yx3+1c. y -x3+3x+1d. y-x3-5x2-9x-4e. yx4-2x2-1f. y -dfrac{x^4}{2}-x2+dfrac{3}{2}g. y2x2-x4
Đọc tiếp
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. y=x3-3x+2
b. y=x3+1
c. y= -x3+3x+1
d. y=-x3-5x2-9x-4
e. y=x4-2x2-1
f. y= \(-\dfrac{x^4}{2}\)-x2+\(\dfrac{3}{2}\)
g. y=2x2-x4
Khảo sát và vẽ đồ thị hàm số a, y=-1/3x^3+1/2x^2-2x+1 b, y= -x^3+3x^2-4 c, y= -1/4x^4-1/2x^2-1/4 d, y= x^4-x^2-2
Iq79
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau
Y = 2+3x-1🤔🤔🤔