Phương trình đã cho tương đương với phương trình:

2(x − k) =  x - 1 2  hoặc 2(x − k) = - x - 1 2

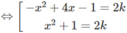
Ta vẽ đồ thị của hai hàm số: y = − x 2  + 4x – 1 và y =  x 2  + 1

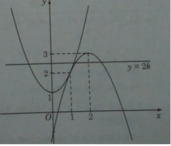
Từ đồ thị ta suy ra:

    • 2k > 3 : phương trình có hai nghiệm;

    • 2k = 3 : phương trình có ba nghiệm;

    • 2 < 2k < 3 : phương trình có bốn nghiệm;

    • 2k = 2 : phương trình có ba nghiệm;

    • 1 < 2k < 2 : phương trình có bốn nghiệm ;

    • 2k = 1 : phương trình có ba nghiệm ;

    • 2k < 1 : phương trình có hai nghiệm.

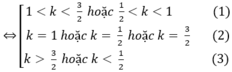
(1) : phương trình có bốn nghiệm;

(2): phương trình có ba nghiệm ;

(3): phương trình có hai nghiệm.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y =  x + 1 2 .(2 − x).

y = − x 3  + 3x + 2 ⇒ y′ = −3 x 2  + 3

y′=0 ⇔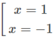 

Bảng biến thiên:

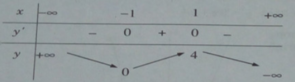
Đồ thị:

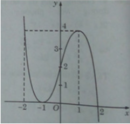
Từ đồ thị hàm số ta suy ra:

    • k > 4 hoặc k < 0: phương trình có một nghiệm;

    • k = 4 hoặc k = 0 : phương trình có hai nghiệm;

    • 0 < k < 4: phương trình có ba nghiệm.

\(mx-x-m+2=0\)

\(x\left(m-1\right)=m-2\)

Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)

Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)

Vậy ...

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]

Bảng biến thiên là:

Phương trình tương đương

\(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)\left(x-2\right)\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)x-2m-2\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}\left(m-1-m-1\right)x=-2m-4\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}-2x=-2m-4\\x\ne2\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}x=m+2\\x\ne2\end{matrix}\right.\)

Nếu m = 0 thì phương trình vô nghiệm

Nếu m ≠ 0 thì S = {m + 2}