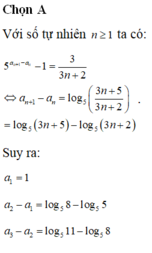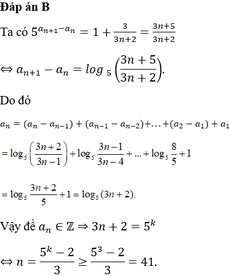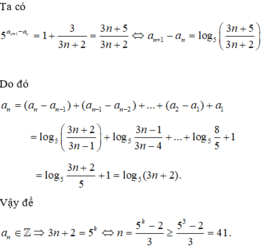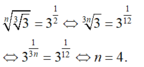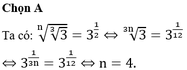Tìm số nguyên n thỏa mãn: 33n+1 = 9n+2

Những câu hỏi liên quan
Cho dãy số
(
a
n
)
thỏa mãn
5
a
n
+
1
-
a
n
3
3
n
+
2
với mọi n
≥...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn 5 a n + 1 - a n = 3 3 n + 2 với mọi n ≥ 1. Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Chọn A
Với số tự nhiên n ≥ 1, ta có:
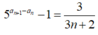
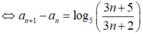
![]()
Suy ra:
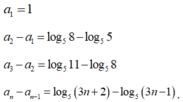
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n
≥
1
với mọi số tự nhiên n
≥
1
Để ![]()
![]()
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
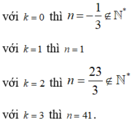
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
Đúng 0
Bình luận (0)
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
3
3
n
+
2...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Cho dãy số
(
a
n
)
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 với mọi n ≥ 1 Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Cho n là một số nguyên dương thỏa mãn
3
3
n
3
1
12
.Tìm giá trị của n. A. n 4 B. n 9 C. n 3 D. n 6
Đọc tiếp
Cho n là một số nguyên dương thỏa mãn 3 3 n = 3 1 12 .Tìm giá trị của n.
A. n = 4
B. n = 9
C. n = 3
D. n = 6
Cho n là một số nguyên dương thỏa mãn 3 3 n = 3 1 12 .Tìm giá trị của n.
A.n=4.
B. n=9.
C. n=3.
D. n=6.
n3+8n2+13nn3+8n2+13nlà số nguyên tố
Đọc tiếp
là số nguyên tố
1.
\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)
\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)
\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)
\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)
Đặt \(xy=a\Rightarrow0< a\le1\)
\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)
\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)
\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)
\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)
\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)
\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)
Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)
Đúng 1
Bình luận (3)
2.
Đặt \(A=9^n+62\)
Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)
Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)
\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)
Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\) và \(6m+1\)
\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)
\(\Leftrightarrow36m^2=9^n+63\)
\(\Leftrightarrow4m^2=9^{n-1}+7\)
\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)
\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)
Pt ước số cơ bản, bạn tự giải tiếp
Đúng 2
Bình luận (2)
tìm tất cả các số nguyên m, n thỏa mãn \(3^{72m^2+9n^2-2015}+10\) là số nguyên tố
Tìm tất cả các số nguyên dương n thỏa mãn:
a) \(n^2+8n+29\) là số chính phương
b) \(9n^2+6n+22\)là số chính phương
a) \(n^2+8n+29=n^2+4n+4n+16+15=\left(n+4\right)^2+15=m^2\)
\(\Leftrightarrow m^2-\left(n+4\right)^2=15\Leftrightarrow\left(m-n-4\right)\left(m+n+4\right)=13=1.13\)
Do \(m-n-4< m+n+4\)nên ta có trường hợp:
\(\hept{\begin{cases}m-n-4=1\\m+n+4=13\end{cases}}\Leftrightarrow\hept{\begin{cases}m=7\\n=2\end{cases}}\)(thỏa)
b) \(9n^2+6n+22=3\left(3n^2+n\right)+3n+1+21=\left(3n+1\right)^2+21=m^2\)
\(\Leftrightarrow m^2-\left(3n+1\right)^2=21\Leftrightarrow\left(m-3n-1\right)\left(m+3n+1\right)=21=1.21=3.7\)
Ta có các trường hợp:
- \(\hept{\begin{cases}m-3n-1=1\\m+3n+1=21\end{cases}}\Leftrightarrow\hept{\begin{cases}m=11\\n=3\end{cases}}\)(thỏa)
- \(\hept{\begin{cases}m-3n-1=3\\m+3n+1=7\end{cases}}\Leftrightarrow\hept{\begin{cases}m=5\\n=\frac{1}{3}\end{cases}}\)(loại)