ko trả lời được vì đề thiếu điều kiện

LÀ SAO NHi 

Đáp án là A.

Gọi x 0 < x < a    là độ dài của một cạnh góc vuông.

Độ dài cạnh góc vuông còn lại là: a − x 2 − x 2 = a 2 − 2 a x .

Diện tích của tam giác là: S = 1 2 x a 2 − 2 a x .

Ta có S ' = 1 2 a 2 − 3 a x a 2 − 2 a x ; ⇒ S ' = 0 ⇔ x = a 3 .

Bảng biến thiên:

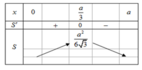
vậy  S max = a 2 6 3

1)396

2)212,8

3)135

4)1111

DÀI THẾ MK CHỊU!!!

số tu nhiên có 3 chữ số khác nhau là:

99x88=132

đáp số:132

a = 60cm

p = 160/2 = 80cm

p = \(\dfrac{a+b+c}{2}\) (1) => \(\dfrac{2p-a}{2}\) = \(\dfrac{b+c}{2}\)

Vì a, p là 1 hằng số nên để S đạt GTLN <=> (p-b) và (p-c) đạt GTLN

Áp dụng bđt Cosin, ta có:

\(\sqrt{\left(p-b\right)\left(p-c\right)}\) <= \(\dfrac{p-b+p-c}{2}\) = \(\dfrac{2p-b-c}{2}\)

=> \(\dfrac{S}{\sqrt{p\left(p-a\right)}}\) <= \(p-\dfrac{b+c}{2}\) = \(p-\dfrac{2p-a}{2}\) = \(\dfrac{a}{2}\)

=> 2S <= \(a\sqrt{p\left(p-a\right)}\) = \(60\sqrt{80.\left(80-60\right)}\) = 2400

=> S <= 1200 (\(cm^2\))

Dấu "=" xảy ra

<=> \(p-b\) = \(p-c\)

<=> b = c

Thay b = c vào (1), ta được:

p = \(\dfrac{a+2b}{2}\) => 80 = \(\dfrac{60+2b}{2}\) => b = c = 50 (cm)

=> đpcm

Từ phương trình mặt phẳng (P) ta có: y = 2x - 2z - 12 nên tọa độ điểm  C a ; 2 a - 2 b ; b

Ta có  A B ⇀ = 1 ; 0 ; 1 , A C → = a - 1 ; 2 a - 2 b - 13 ; v - 3

Suy ra  A B ⇀ , A C ⇀ = 2 a - 2 b - 13 ; b - a - 2 ; 13 - 2 a + 2 b

Do đó 

S A B C = 1 2 A B ⇀ , A C ⇀ = 1 2 2 a - 2 b - 13 2 + b - a - 2 2 + 13 - 2 a + 2 b 2

Đặt t = a - b thì

4 S ∆ A B C 2 = 2 t - 13 2 + t + 2 2 + 13 - 2 t 2 = 9 t 2 - 100 t + 342 = 30 t - 50 3 2 + 578 9 ≥ 578 9

Dấu “=” xảy ra khi và chỉ khi  t = 50 9

Do đó m i n S A B C = 17 2 6  khi t = 50 9 . Vì thế  b = a - 50 9

Suy ra  C a ; - 8 9 ; a - 50 9

Vậy tập hợp các điểm C là đường thẳng có phương trình  x = t y = - 8 9 z = - 8 9 + t

Đáp án B