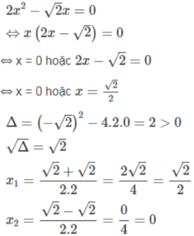Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được: 2 x + 5 y = 2 2 5 x + y = 1

Những câu hỏi liên quan
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được:
0
,
2
x
+
0
,
1
y
0
,
3
3...
Đọc tiếp
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được: 0 , 2 x + 0 , 1 y = 0 , 3 3 x + y = 5
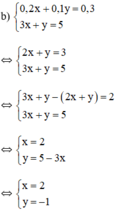
Vậy hệ phương trình có nghiệm duy nhất (2; -1).

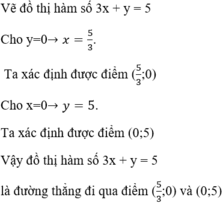
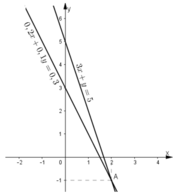
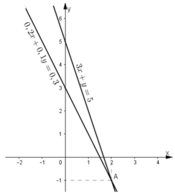
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được:
3
2
x
-
y
1
2
3
x
-
2
y...
Đọc tiếp
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được: 3 2 x - y = 1 2 3 x - 2 y = 1
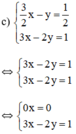
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng 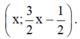


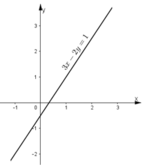
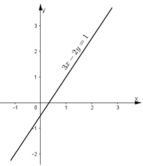
KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau và minh họa bằng hình học kết quả tìm được:
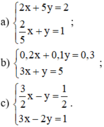
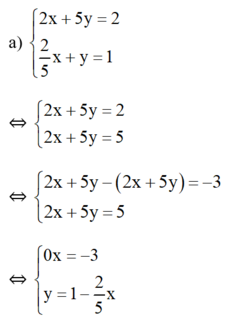
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
Minh họa hình học:
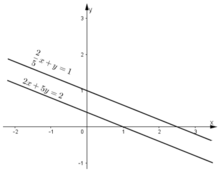
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng 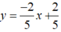 (d1)
(d1)
Tập nghiệm của phương trình 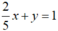 được biểu diễn bởi đường thẳng
được biểu diễn bởi đường thẳng 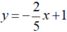 (d2).
(d2).


KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm
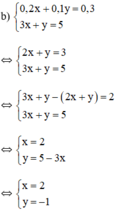
Vậy hệ phương trình có nghiệm duy nhất (2; -1).

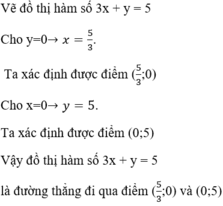
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
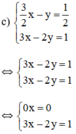
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng 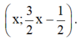


KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm
Đúng 0
Bình luận (0)
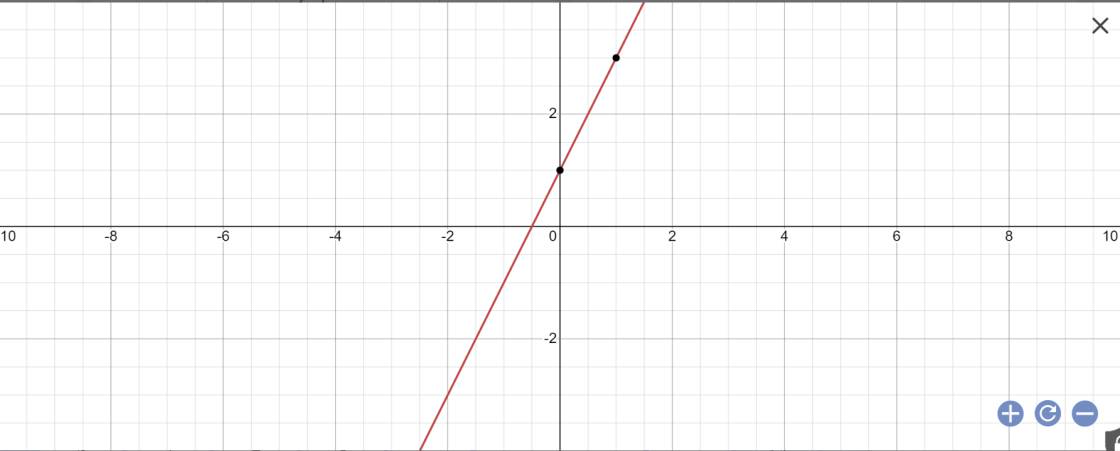
Hãy minh họa bằng hình học tập nghiệm của hệ phương trình (1 ) x + y = 4 ; ( 2 ) 2x - y = -1
(1): x+y=4
=>y=4-x
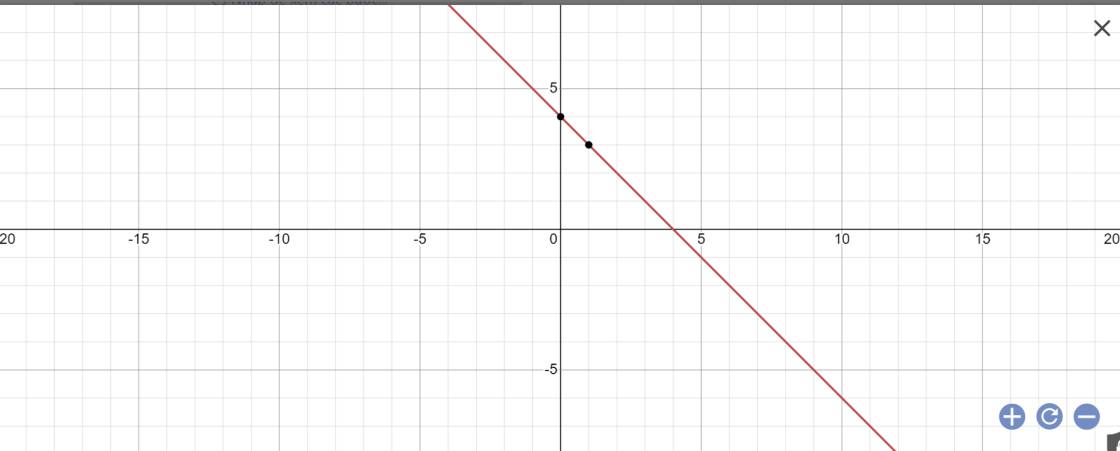
(2): 2x-y=-1
=>y=2x+1
Đúng 1
Bình luận (0)
Giải các phương trình sau bằng hai cách (phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được: 2 x 2 - 2 x = 0
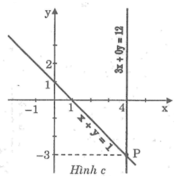
Minh họa hình học tập nghiệm của mỗi hệ phương trình sau: x + y = 1 3 x + 0 y = 12
*Ta có: x + y = 1 ⇔ y = -x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1 ⇒ (1; 0)
*Ta có: 3x + 0y = 12 ⇔ x = 4
Hai đường thẳng cắt nhau tại P(4; -3) nên nghiệm của hệ phương trình là (x; y) = (4; -3)
Đồ thị:
Đúng 0
Bình luận (0)
Cho hệ phương trình
I
V
4
x
+
y
2
8
x
+
2
y
1
Bằng minh h...
Đọc tiếp
Cho hệ phương trình I V 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
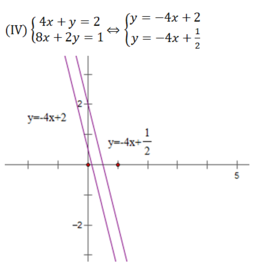
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
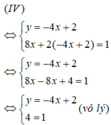
Vậy hệ phương trình (IV) vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng hai cách (phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được: 5 x 2 - 3x = 0
Cho hệ phương trình
(IV)
4
x
+
y
2
8
x
+
2
y
1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
Đọc tiếp
Cho hệ phương trình
(IV) 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
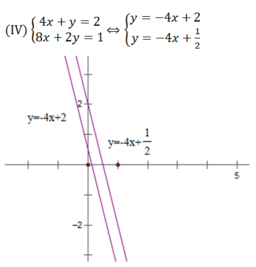
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
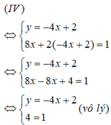
Vậy hệ phương trình (IV) vô nghiệm.
Đúng 0
Bình luận (0)