a/ Gọi điểm cố định \(M\left(x_0;y_0\right)\)

Khi đó đường thẳng y = k(x+3)-7 đi qua M , tức \(k\left(x_0+3\right)-7-y_0=0\) 

Vì đường thẳng y = k(x+3)-7 luôn đi qua M nên \(\hept{\begin{cases}x_0+3=0\\-y_0-7=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-3\\y_0=-7\end{cases}}\)

Vậy đường thẳng đã cho luôn đi qua điểm M(-3;-7)

b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)

Vì họ đường thẳng (m+2)x + (m-3)y -m+8 = 0 luôn đi qua N nên : 

\(\left(m+2\right).x_0+\left(m-3\right).y_0-m+8=0\)

\(\Leftrightarrow m\left(x_0+y_0-1\right)+\left(2x_0-3y_0+8\right)=0\)

Ta có \(\hept{\begin{cases}x_0+y_0-1=0\\2x_0-3y_0+8=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=2\end{cases}}\)

Vậy điểm cố định N(-1;2)

Câu còn lại bạn làm tương tự nhé ^^

c/ Đơn giản thôi mà =)

Ta cũng gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)

Vì họ đường thẳng y=(2-k)x+k-5 đi qua M nên : 

\(y_0=\left(2-k\right)x_0+k-5\Leftrightarrow k\left(1-x_0\right)+\left(2x_0-y_0-5\right)=0\)

Ta có \(\hept{\begin{cases}1-x_0=0\\2x_0-y_0-5=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=1\\y_0=-3\end{cases}}\)

Vậy điểm cố định là M(1;-3)

Gọi M ( x 0 ;   y 0 )  là điểm cố định mà d luôn đi qua.

  M   ( x 0 ;   y 0 )     ∈ d     ∀     k

⇔ y 0 = k + 1 3 − 1 x 0 + k + 3 ∀ k ⇔ k x 0 + x 0 + 3 k − k − 3 + 3 − 3 y 0 + y 0 = 0 ∀ k ⇔ k x 0 + 3 − 1 + x 0 + 3 − 3 + 1 − 3 y 0 = 0   ∀ k ⇔ x 0 + 3 − 1 = 0 x 0 + 1 − 3 y 0 + 3 − 3 = 0 ⇔ x 0 = 1 − 3 1 − 3 + 1 − 3 y 0 + 3 − 3 = 0 ⇔ x 0 = 1 − 3 1 − 3 y 0 + 4 − 2 3 = 0 ⇔ x 0 = 1 − 3 1 − 3 y 0 + 1 − 3 2 = 0 ⇔ x 0 = 1 − 3 y 0 = − 1 + 3 ⇒ M 1 − 3 ; 3 − 1

 là điểm cố định mà d luôn đi qua

Đáp án cần chọn là: A

 Với k ≥ 0 ta có:

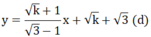
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua

Khi đó ta có:

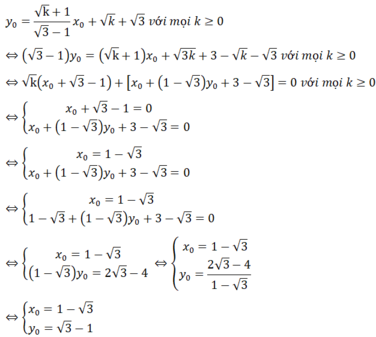
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ;  3 -1)

Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o ,  y o ).

Ta có:

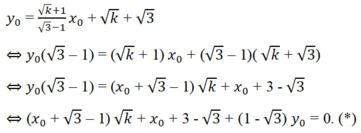
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:

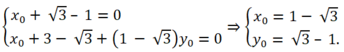
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1-  3 ;  3  – 1).

Tam giác ABC vuông tại A \(\Rightarrow R=\frac{BC}{2}=\frac{1}{2}\sqrt{6^2+8^2}=5\)

a. Gọi \(d_1\)là đường thẳng cần tìm 

Vì \(d_1\)song song Ox nên \(d_1\)có dạng y=b. Vì \(d_1\)đi qua K(-1;8) \(\Rightarrow d_1:y=8\)

b. Gọi \(d_2\)là đường thẳng đi qua M.N \(\Rightarrow\hept{\begin{cases}-3=1.a+b\\2=0+b\end{cases}\Rightarrow\hept{\begin{cases}a=-5\\b=2\end{cases}}}\)

\(\Rightarrow d_2:y=-5x+2\)

Gọi d là đường thẳng cần  tìm .Vì d song song  \(d_2\)\(\Rightarrow d:y=-5x+b\)

d đi qua gốc tọa độ  \(\Rightarrow b=0\)

Vậy d có dạng y=-5x

Gọi đường thẳng (d) có hàm số y=kx+b (k khác 0) (do hàm số có hệ số góc là k )

Vì (d) đi qua I(0;-1) => -1=0k+b => b=-1

=> y=kx-1(d)

Xét phương trình hoành độ giao điểm chung của (P) và (d) ta có:

-x^2=kx-1

<=> x^2-kx-1=0 (1)

Xét phương trình có a=1;c=-1 => ac=-1 <0 

=> (1) luôn có 2 nghiệm phân biệt

=> (P) và (d) luôn cắt nhau tại 2 điểm phân biệt