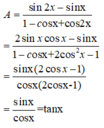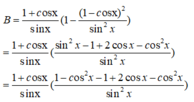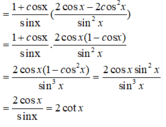Rút gọn các biểu thức sau: 1 - a a 1 - a v ớ i a ≥ 0 v à a ≠ 1

Những câu hỏi liên quan
Tìm x để các biểu thức sau có nghĩa và rút gọn các biểu thức sau: a) x-√x /√x-1 - x-1/√x+1
\(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\);\(ĐK:x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow\sqrt{x}-\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+1\)
\(\Leftrightarrow1\)
Đúng 2
Bình luận (0)
a: \(=\sqrt{x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1=1\)
Đúng 2
Bình luận (0)
Rút gọn các biểu thức sau: 27 . 48 . 1 - a 2 v ớ i a > 1
27 . 48 1 - a 2 = 9 . 3 . 3 . 16 . 1 - a 2

Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau:
A
sin
2
x
-
sin
x
1
-
c
o
t
x
+
cos
2
x
B
1
+
cos
x
sin
x
(
1...
Đọc tiếp
Rút gọn các biểu thức sau:
A = sin 2 x - sin x 1 - c o t x + cos 2 x B = 1 + cos x sin x ( 1 - ( 1 - cos x ) 2 sin 2 x )
Rút gọn các biểu thức sau:
\(C=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{1}}\right):\dfrac{\sqrt{a}+1}{a-1}\)
ĐK: `a \ne 1 ; a>=0`
`C=(\sqrta/(\sqrta-1)-\sqrta/(a-1)) : (\sqrta+1)/(a-1)`
`=(\sqrta/(\sqrta-1) - \sqrta/((\sqrta-1)(\sqrta+1))) . (a-1)/(\sqrta+1)`
`= (\sqrta(\sqrta+1)-\sqrta)/((\sqrta-1)(\sqrta+1)) . ((\sqrta-1)(\sqrta+1))/(\sqrta+1)`
`= a/(\sqrta+1)`
Đúng 4
Bình luận (0)
Ta có: \(C=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-1}\right):\dfrac{\sqrt{a}+1}{a-1}\)
\(=\dfrac{a+\sqrt{a}-\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}:\dfrac{1}{\sqrt{a}-1}\)
\(=\dfrac{a}{\sqrt{a}+1}\)
Đúng 3
Bình luận (1)
Rút gọn rồi tính giá trị các biểu thức sau: 1 - 10 a - 25 a 2 - 4 a t ạ i a = 2
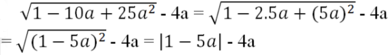
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau: A=\(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}-1}+1}\)
\(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}-1}+1}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1\right)}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}-1}-1\right)}{\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\right)}{\sqrt{3}}=\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\)
Đúng 1
Bình luận (2)
Rút gọn biểu thức sau: (1- cos a) ( 1+ cos a)
Xem chi tiết
ta có :
\(\left(1-cosa\right)\left(1+cosa\right)=1-cos^2a=sin^2a\)
Bài 1 (2điểm)1) Nêu điều kiện để √a có nghĩa ?2) Áp dụng: Tìm x để các căn thức sau có nghĩa:Bài 2: ( 3 điểm ): Rút gọn biểu thứcBài 3 ( 4 điểm ) Cho biểu thức(Với x 0; x 1; x4)a/ Rút gọn P.b/ Với giá trị nào của x thì P có giá trị bằng 1/4c/ Tính giá trị của P tại x 4 + 2√3d/ Tìm số nguyên x để biểu thức P có giá trị là số nguyên ?Bài 4 : ( 1 điểm ): ChoTìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Đọc tiếp
Bài 1 (2điểm)
1) Nêu điều kiện để √a có nghĩa ?
2) Áp dụng: Tìm x để các căn thức sau có nghĩa:
![]()
Bài 2: ( 3 điểm ): Rút gọn biểu thức

Bài 3 ( 4 điểm ) Cho biểu thức
 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)
a/ Rút gọn P.
b/ Với giá trị nào của x thì P có giá trị bằng 1/4
c/ Tính giá trị của P tại x = 4 + 2√3
d/ Tìm số nguyên x để biểu thức P có giá trị là số nguyên ?
Bài 4 : ( 1 điểm ): Cho
![]()
Tìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)
a) \(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}\)
b) \(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}\)
làm chi tiết hộ em ạ
\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
Đúng 0
Bình luận (0)
a: \(=-\sqrt{a}\)
b: \(=\sqrt{p}\)
Đúng 0
Bình luận (0)