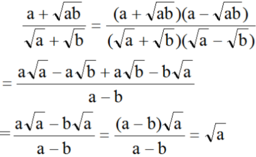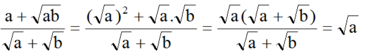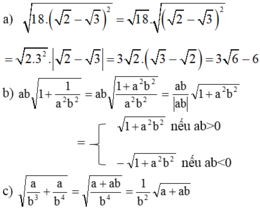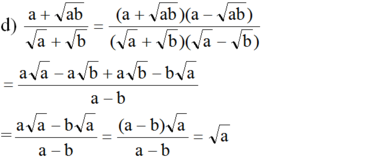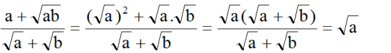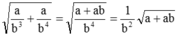Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a b 1 + 1 a 2 b 2
Những câu hỏi liên quan
Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a + a b a + b
Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa):
a
)
18
2
-
3
2
b
)
a
b
1
+
1
a
2
b
2
c
)
...
Đọc tiếp
Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa):
a ) 18 2 - 3 2 b ) a b 1 + 1 a 2 b 2 c ) a b 3 + a b 4 d ) a + a b a + b
9 tháng 11 2021 lúc 20:48
rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)
a) \(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}\)
b) \(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}\)
làm chi tiết hộ em ạ
\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
Đúng 0
Bình luận (0)
a: \(=-\sqrt{a}\)
b: \(=\sqrt{p}\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): 18 2 - 3 2
Rút gọn các biểu thức sau (giả thiết biểu thức chữ đều có nghĩa): a b 3 + a b 4
Rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa):
2
+
2
1
+
2
;
15
-
5
1
-
3
;
2
3
-
6...
Đọc tiếp
Rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa):
2 + 2 1 + 2 ; 15 - 5 1 - 3 ; 2 3 - 6 8 - 2 ; a - a 1 - a ; p - 2 p p - 2
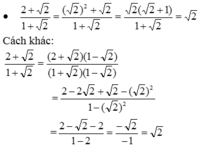
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
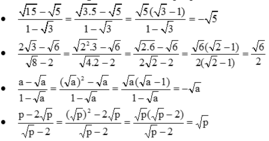
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa):
2
+
2
1
+
2
;
15
-
5
1
-
3
;
2...
Đọc tiếp
Rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa): 2 + 2 1 + 2 ; 15 - 5 1 - 3 ; 2 3 - 6 8 - 2 ; a - a 1 - a ; p - 2 p p - 2
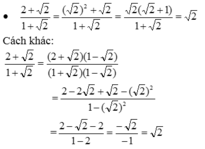
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
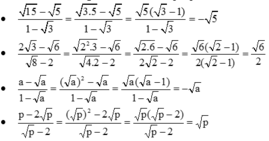
Đúng 0
Bình luận (0)
9 tháng 11 2021 lúc 14:53
rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)
a) \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\)
b) \(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\)
c) \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}\)
\(a,=\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\\ c,=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
Đúng 2
Bình luận (0)
rút gọn biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa): \(\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}=\sqrt{a}\)
Đúng 0
Bình luận (0)
\(\frac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}=\frac{\left(a+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{\left(a+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{a-b}\)
Đúng 0
Bình luận (0)