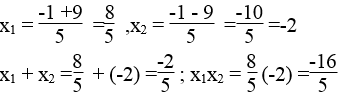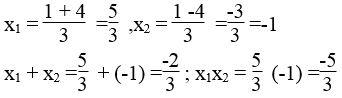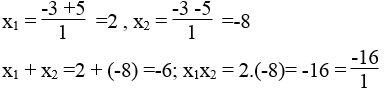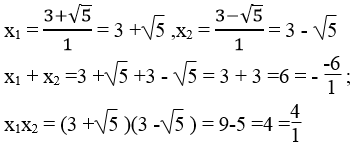Giải phương trình rồi kiểm nghiệm hệ thức vi-ét: 3 x 2 -2x -5 =0

Những câu hỏi liên quan
Giải phương trình rồi kiểm nghiệm hệ thức vi-ét: 5 x 2 + 2x -16 =0
Phương trình 5 x 2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: ∆ '= 1 2 -5(-16) = 1 + 80 =81 >0
∆ ' = 81 =9
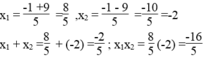
Đúng 0
Bình luận (0)
Giải phương trình rồi kiểm nghiệm hệ thức vi-ét: 1 3 x 2 + 2 x - 16 3 = 0
Phương trình 1 3 x 2 + 2 x - 16 3 = 0 ⇔ x 2 +6x – 16 = 0 có hệ số a = 1, b = 6, c = -16
∆ '= 3 2 -1(-16) = 9 +16 =25 > 0
∆ ' = 25 =5
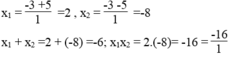
Đúng 0
Bình luận (0)
Giải phương trình rồi kiểm nghiệm hệ thức vi-ét: 1 2 x 2 - 3 x + 2 = 0
Phương trình 1 2 x 2 - 3 x + 2 = 0 ⇔ x 2 - 6x + 4 =0 có hệ số a = 1, b = -6, c = 4
∆ '= - 3 2 -1.4 = 9 - 4 = 5 > 0
∆ ' = 5
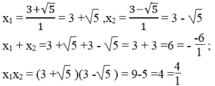
Đúng 0
Bình luận (0)
Giải phương trình rồi kiểm nghiệm hệ thức Vi-ét :
a) \(3x^2-2x-5=0\)
b) \(5x^2+2x-16=0\)
c) \(\dfrac{1}{3}x^2+2x-\dfrac{16}{3}=0\)
d) \(\dfrac{1}{2}x^2-3x+2=0\)
a, \(3x^2-2x-5=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\times3\times\left(-5\right)\)
\(\Rightarrow\Delta=4+60\)
\(\Rightarrow\Delta=64\)
\(\Rightarrow\sqrt{\Delta}=8\)
vậy phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{2+64}{6}=11\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{2-64}{6}=\dfrac{-62}{6}=\dfrac{-31}{3}\)
b, \(5x^2+2x-16\)
\(\Rightarrow\Delta=2^2-4\times5\times\left(-16\right)\)
\(\Rightarrow\Delta=4+140\)
\(\Rightarrow\Delta=144\)
\(\Rightarrow\sqrt{\Delta}=12\)
vậyphương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-2+12}{10}=\dfrac{10}{10}=1\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-2-12}{10}=\dfrac{-14}{10}=\dfrac{-7}{5}\)
Đúng 0
Bình luận (0)
Dùng hệ thức vi-ét để tìm nghiệm x 2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau: Phương trình x 2 - 2(m -3)x + 5 =0 có nghiệm x 1 =1/3
Theo hệ thức Vi-ét ta có: x 1 x 2 =5/3
Suy ra: 1/3 . x 2 = 5/3 ⇔ x 2 =5/3 : 1/3 =5/3 .3=5
cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =[2(m -3)]/3
Suy ra: 1/3 +5 = [2(m -3)]/3 ⇔ 2(m -3) =16 ⇔ m-3=8 ⇔ m=11
Vậy với m = 11 thì phương trình 3 x 2 -2(m -3)x +5 =0 có hai nghiệm x 1 = 1/3 , x 2 = 5
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 5 x 2 + x + 2 = 0
Ta có: ∆ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
: Giải phương trình rồi kiểm nghiệm hệ vi-ét:
a. 5x2 + 2x -16 =0 b.3x2 -2x -5 =0
Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0
Δ' = 81 =9
Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5
Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0
Δ' = 16 =4
Phương trình 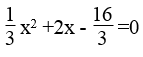
Δ'=32 -1(-16) = 9 +16 =25 > 0
Δ' = 25 =5
Phương trình 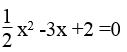
Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0
Δ' = 5
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình (2 - 3 ) x 2 + 4x + 2 + 2 = 0
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
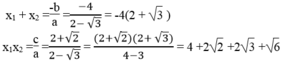
Đúng 0
Bình luận (0)
Cho phương trình:-2x2 +3x+6=0
Không giải phương trình, hãy tính giá trị biểu thức |x1-x2| biết x1, x2 là nghiệm của PT trên.
*Giải bằng Hệ thức Vi-ét!
Vì P = 6 / -2 = -3 < 0
=> Phương trình có hai nghiệm trái dấu
Áp dụng định lí Viet ta có:
\(\hept{\begin{cases}x_1x_2=\frac{6}{-2}\\x_1+x_2=\frac{3}{2}\end{cases}}\)
Ta có: \(\left|x_1-x_2\right|^2=\left(x_1+x_2\right)^2-4x_1x_2=\left(\frac{3}{2}\right)^2-4\left(\frac{6}{-2}\right)=\frac{57}{4}\)
=> \(\left|x_1-x_2\right|=\frac{\sqrt{57}}{2}\)