B. Phần tự luận (6 điểm)
Cho tam giác ABC có A B = 3 c m , A C = 4 c m , B C = 5 c m
a. Tam giác ABC là tam giác gì? Vì sao
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Biết
∠ A = 55 o , ∠ B = 67 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
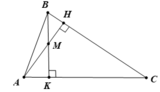
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Biết
∠ A = 55 o , ∠ B = 67 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
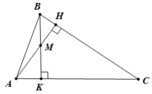
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
a. Tính góc( BIC)
a. Hình vẽ ( 0.5 điểm )
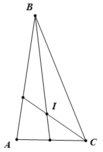
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
B. Phần tự luận (6 điểm)
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
a. Tính góc( BIC)
a. Hình vẽ ( 0.5 điểm )
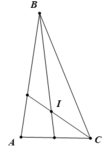
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
Cho tam giác ABC có tọa độ 3 đinh là A(4; 1), B(3; 2), C(1; 6).Viết phương trình: g) đường thẳng qua C và chia tam giác thành hai phần, phần chứa điểm A có diện tích gấp đối phần chứa điểm B.
Phương trình đường thẳng qua điểm C là: 5x + 3y - 21 = 0
Tìm điểm D trên đường thẳng BC sao cho AD là đường cao của tam giác ABC.
Diện tích tam giác ABD là: \(S_{ABD} = \dfrac{1}{2} \cdot 1 \cdot \dfrac{2}{3} = \dfrac{1}{3}\)
Diện tích phần chứa điểm B là: \(S_{BCD} = \dfrac{1}{3}\)
Diện tích phần chứa điểm A là: \(S_{ACD} = S_{ABC} - S_{ABD} - S_{BCD} = \dfrac{1}{2} \cdot 1 \cdot \sqrt{26} - \dfrac{1}{3} - \dfrac{1}{3} = \dfrac{1}{2} \cdot \sqrt{26} - \dfrac{2}{3}\)
Vậy ta cần tìm điểm D sao cho AD là đường cao của tam giác ABC và \(S_{ACD} = 2S_{BCD}\)
Giải hệ phương trình tìm được D(2;4).
Vậy phương trình đường thẳng chia tam giác thành hai phần, phần chứa điểm A có diện tích gấp đôi phần chứa điểm B là: 5x - 3y - 7 = 0.
B. Phần tự luận (6 điểm)
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a. Chứng minh ΔAMB = ΔDMC
a. Hình vẽ (1 điểm)

Xét ΔABM và ΔBCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔBCM (c.g.c) (1 điểm)
Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH
a) Tính BC, AH, ∠B ; ∠C
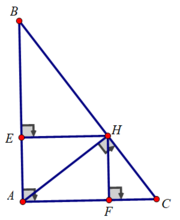
a) Xét tam giác ABC vuông tại A có:
A
B
2
+
A
C
2
=
B
C
2
⇒ 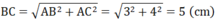
Ta có:
AH.BC = AB.AC ⇒ 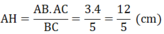
sinB = AC/BC = 4/5 ⇒ ∠B = 53 , 1 0
⇒ ∠C = 90 0 - ∠B = 36 , 9 0
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
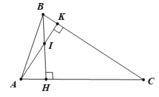
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)