Tam giác ABC có ∠ A = 80 o , ∠ B = 40 o . Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là:
A. 100 o
B. 80 o
C. 60 o
D. 30 o
: Tam giác ABC có các góc A, B , C lần lượt tỉ lệ với các số 2; 3 và 4 thì số đo các góc của tam giác ABC là:
A. góc A bằng 40\(^o\); góc B bằng 60\(^o\) ; góc C bằng 80\(^o\)
B. góc A bằng 30\(^o\) ; góc B bằng 70\(^o\); góc C bằng 80\(^o\)
C. góc A bằng 80\(^o\); góc B bằng 60\(^o\); góc C bằng 40\(^o\)
A. góc A bằng 40*; góc B bằng 60*; góc C bằng 80*
Cho tam giác ABC . Các tia phân giác góc B,C cắt nhau ở I .
Tính góc BTC biết:
a) Góc B = 80o ; góc C = 40o
b) Góc A = 80o
a) ta có BIC=180-IBC-ICB=180-1/2B-1/2C
=180-1/2(B+C)=180-1/2.(80+40)=180-1/2.120=180-60=120
vậy BIC=120 độ
b) ta chứng minh tương tự như trên
BIC=180-1/2(B+C)=180-1/2(180-A)=180-1/2.100
=180-50=130
vậy BIC =130
cho tam giác ABC có góc B =\(40^o\)góc C\(=30^o\)bên ngoài tam giác ABC dựng tam giác ADC cân tại D và ADC= \(80^o\)CMR tam giác BAD cân
Cho tam giác ABC có góc A = 80°, góc B = 60°, O là giao điểm các đường trung trực của tam giác ABC. Tính số đo góc OAB.
Giúp mình với!!!
Cho tam giác ABC có \(\widehat{A}\)= 60o; \(\widehat{B}\)= 80o và có phân giác AD
a) So sánh các cạnh của tam giác ADC
b) So sánh các cạnh của tam giác ADB
thôi nha mik tự làm đc r
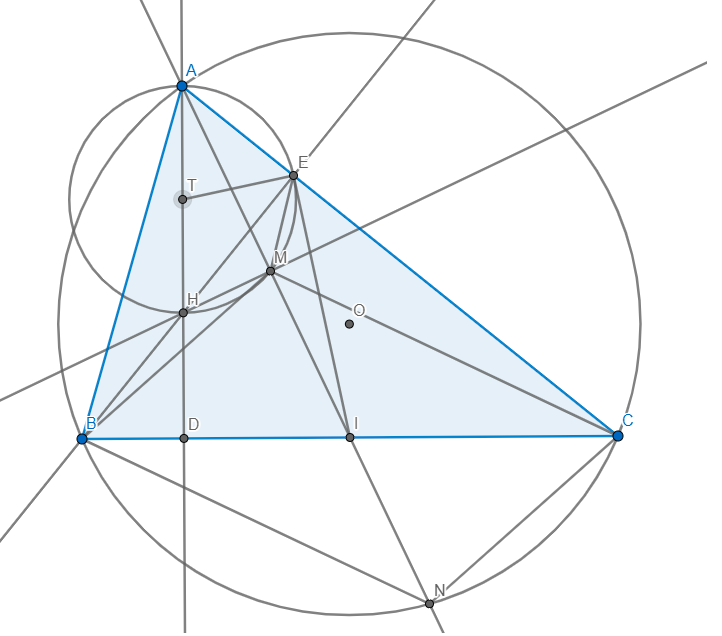
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I là trung điểm của BC, vẽ HM vuông góc cới AI tại M.
a) Chửng minh tứ giác AHME nội tiếp và AE.AC = AM.AI;
b) Đường thẳng AI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh I là trung điểm của đoạn thẳng MN.
a) Ta có: \(\angle AMH=\angle AEH=90\Rightarrow AEMH\) nội tiếp
\(\Rightarrow\angle AME=\angle AHE\)
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HECD\) nội tiếp
\(\Rightarrow\angle AHE=\angle ACD\Rightarrow\angle AME=\angle ACD\Rightarrow MECI\) nội tiếp
\(\Rightarrow\angle AME=\angle ACI\)
Xét \(\Delta AME\) và \(\Delta ACI:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACI\\\angle CAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACI\left(g-g\right)\Rightarrow\dfrac{AM}{AC}=\dfrac{AE}{AI}\Rightarrow AE.AC=AM.AI\)
b) Gọi T là trung điểm AH
Dễ dàng chứng minh được T là tâm (AEMH)
\(\Rightarrow\Delta TEH\) cân tại T \(\Rightarrow\angle TEH=\angle THE=\angle ACB\) (HECD nội tiếp)
\(\Delta EBC\) vuông tại E có I là trung điểm BC cân tại I
\(\Rightarrow\Delta EBI\) cân tại I \(\Rightarrow\angle BEI=\angle EBI\)
mà \(\angle EBI+\angle ACB=90\Rightarrow\angle BEI+\angle TEH=90\Rightarrow\angle TEI=90\)
\(\Rightarrow IE\) là tiếp tuyến của (AEMH)
\(\Rightarrow\angle IAE=\angle IEM=\angle ICM\) (EMIC nội tiếp)
mà \(\angle IAE=\angle NBC\) (NBAC nội tiếp) \(\Rightarrow\angle ICM=\angle NBC\)
\(\Rightarrow CM\parallel BN\)
Tương tự \(\Rightarrow BM\parallel CN\) \(\Rightarrow BMCN\) là hình bình hành
mà I là trung điểm BC \(\Rightarrow I\) là trung điểm MN
Cho tam giác ABC vuông tại C có AB =5cm,ABC =60°, đường cao CK.Vẽ đường tròn tâm O đường kính CK , đường tròn (O ) cắt CB tại P (P khác C) a) Tính độ dài đoạn thẳng BC b) Chứng minh AB là tiếp tuyến của đường tròn (O) c)Tính khoảng cách từ O đến đường thẳng BC d) Từ B vẽ tiếp tuyến thứ hai BH với đường tròn (O) (H là tiếp điểm , H khác K ).Chứng minh tam giác BHP đồng dạng với tam giác BHC.
a: Xét ΔABC vuông tại C có
\(BC=AB\cdot\sin30^0=5\cdot\dfrac{1}{2}=2.5\left(cm\right)\)
1. Cho tam giác ABC có góc B= 80 độ, C=40 độ. Phân giác Góc B cắt phân giác góc C tại O, cắt cạnh AC ở D, AB ở E
a, Tìm số đo các góc BOE và COD
b, C/m OD=OE
gocBOE=COD=(80 +40) : 2= 60o
(OD khac OE de bai sai)
Cho tam giác ABC có góc B = 80 độ, góc C = 40 độ. Phân giác của góc B cắt phân giác của góc C tại O cắt cạnh AC tại D. Phân giác của góc C cắt cạnh AB tại E
a) Tính số đó các góc BOE và COD
b) Chứng minh rằng OD = OE