Cho hàm số y = f x xác định, có đạo hàm liên tục trên ℝ , thỏa mãn f 2 x = 4 f x cos x - 2 x với mọi x ∈ ℝ . Phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục tung.
A. y = 2 - x
B. y = -x
C. y = x
D. y = 2x - 1
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn x f ( x ) . f ' ( x ) = f 2 ( x ) - x , ∀ x ∈ ℝ và f(2)=1 .Tích phân bằng
A. 3 2
B. 4 3
C. 2
D. 4
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
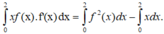
Tích phân từng phần có
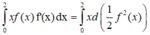
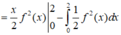
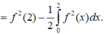
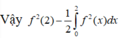
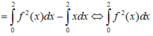
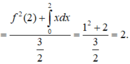
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ thỏa mãn f ' x - x f x = 0 , f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e
B. 1 e
C. e
D. e
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ thỏa mãn f 2 = - 2 ; ∫ 0 2 f x d x = 1 . Tính tích phân I = ∫ 0 4 f ' x d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Đáp án A
Đặt t = x ⇔ d t = d x 2 x ⇔ d x = 2 d t ; x = 0 ⇒ t = 0 x = 4 ⇒ t = 2
Khi đó I = ∫ 0 4 f ' x d x = ∫ 0 2 2 t . f ' t d t = 2 ∫ 0 2 t . f ' t d t
Đặt u = t d v = f ' t d t ⇔ d u = d t v = f t ⇒ 2 ∫ 0 2 t . f ' t d t = t . f t 0 2 - ∫ 0 2 f t d t = 2 f 2 - 1 = - 5
Vậy tích phân I = 2 . - 5 = - 10 .
Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm f '(x) thỏa mãn f ' x = 1 - x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞
Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

![]()
![]()
![]()
![]()
Hàm số y = f ( x ) xác định và liên tục trên R có đạo hàm f ' ( x ) = x - 1 3 x - 2 2 x 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số y = f ( x ) là
A. 3
B. 1
C. 0
D. 2
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ, thỏa mãn 2 f 2 x + f 1 - 2 x = 12 x 2 . Tìm phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=1
A. y=2x+2
B. y=4x-6
C. y=2x-6
D. y=4x-2
Cho hàm số y = f(x) xác định và liên tục trên ℝ \ { 0 } thỏa mãn: x 2 f 2 ( x ) + ( 2 x - 1 ) f ( x ) = x f ' ( x ) - 1 đồng thời f ( 1 ) = - 2 Tính ∫ 1 2 f ( x ) d x
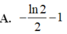
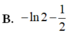
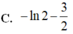
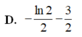
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ , thỏa mãn 2 f 2 x + f 1 - 2 x = 12 x 2 . Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ bằng 1 là
A. y=2x+2
B. y=4x-6
C. y=2x-6
D. y=4x-2