Giải phương trình z 2 + 4 z + 9 = 0 .
A. z = − 2 − i 5 hoặc z = - 2 + i 5
B. z = 2 − i 5 hoặc z = 2 + i 5
C. z = 2 − i 5 hoặc z = 2 + i 5
D. z = − 2 − i 5 2 hoặc z = − 2 + i 5 2
Những câu hỏi liên quan
Dùng phương pháp bất đẳng thức để giải phương trình sau (x^2+1)(y^2+4)(z^2+9)=48xyz(x;y;z>0)
Em học lớp 6 vào chtt nha tick cho em với
Đúng 0
Bình luận (0)
Giải các phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 0 A. z -1; z 2
Đọc tiếp
Giải các phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 = 0
A. z = -1; z = 2
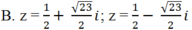
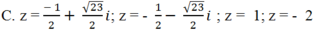
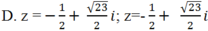
Chọn C.
Đặt t = z2 + z; Phương trình đã cho trở thành
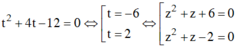
Với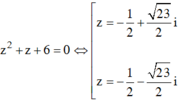 
Với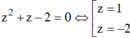 
Vậy phương trình đã cho có 4 nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau trên tập hơn số phức :
a) \(z^4+z^2-6=0\)
b) \(z^4+7z^2+10=0\)
a) Đặt Z = z2 , ta được phương trình Z2 + Z – 6 = 0
Phương trình này có hai nghiệm là Z1 = 2, Z2 = -3
Vậy phương trình có bốn nghiệm là ± √2 và ± i√3.
b) Đặt Z = z2 , ta được phương trình Z2 + 7Z + 10 = 0
Phương trình này có hai nghiệm là Z1 = -5, Z2 = -2
Vậy phương trình có bốn nghiệm là ± i√2 và ± i√5.
Đúng 0
Bình luận (0)
Giải hệ phương trình :\(\left\{{}\begin{matrix}x+xy+y=1\\y+yz+z=4\\z+xz+x=9\end{matrix}\right.\) trong đó x,y,z>0
\(\Leftrightarrow\left\{{}\begin{matrix}xy+x+y+1=2\\yz+y+z+1=5\\zx+z+x+1=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)\left(y+1\right)=2\\\left(y+1\right)\left(z+1\right)=5\\\left(z+1\right)\left(x+1\right)=10\end{matrix}\right.\) (1)
Nhân vế với vế: \(\left[\left(x+1\right)\left(y+1\right)\left(z+1\right)\right]^2=100\)
\(\Leftrightarrow\left(x+1\right)\left(y+1\right)\left(z+1\right)=10\) (2)
Chia vế cho vế của (2) cho từng pt của (1):
\(\Rightarrow\left\{{}\begin{matrix}z+1=5\\x+1=2\\y+1=1\end{matrix}\right.\) \(\Rightarrow\left(x;y;z\right)=\left(1;0;4\right)\) (loại)
Hệ vô nghiệm do \(y>0\)
Đúng 0
Bình luận (0)
Giải phương trình :
\(y^2+4^z+2y-2^{z+1}+2=0\)
Giải phương trình :(y- 4,5 )^4 + (y-5,5 )^4 -1 = 0Tìm nghiệm nguyên của phương trình : 3x^2 + 5y^2 =345Rút gọn phân thức : (x^3 + y^3 -z^3-3xyz ) / (x+y)^2 + (y+z)^2 + (z+x)^2Cho x+y+z=0 . CMr x^3 + y^3 +z^3 =3xyza
Xem chi tiết
Giúp mk giải bài này vs @@ . Ai giải chi tiết mk sẽ tick cho <3 <3
Giải các phương trình, hệ phương trình sau:
a) \(x^4-2ax^2+x+a^2-a=0\)( a là tham số )
b)\(\hept{\begin{cases}xy=x+y-z\\xz=2\left(x-y+z\right)\\yz=3\left(y+z-x\right)\end{cases}}\)
em vẫn chưa lp 9 nên e ko trả lời đk,em xin lỗi kk
Đúng 0
Bình luận (0)
Giải hệ phương trình: x-12/4=y-9/3=z-1 và 3x+5y-z=2
đúng là cái đồ cắt moi mình mới học lớp 3 thôi mà
\(\hept{\begin{cases}x-\frac{12}{4}=y-\frac{9}{3}=z-1\left(1\right)\\3x+5y-z=2\left(2\right)\end{cases}}\)
từ (1), ta có: \(x-\frac{12}{4}=y-\frac{9}{3}\Rightarrow y=x-\frac{12}{4}+\frac{9}{3}=x\Rightarrow y=x\)
lại có: \(x-\frac{12}{4}=z-1\Rightarrow z=x-\frac{12}{4}+1=x-2\Rightarrow z=x-2\)
từ (2), ta rút y, z theo x, ta được: \(3x+5x-x+2=2\Rightarrow7x=0\Rightarrow x=y=0\)
\(\Rightarrow z=x-2=0-2=-2\)
vậy (x;y;z)=(0;0;-2)
a) Giải Phương trình: \(\frac{\sqrt{x-2009}-1}{x-2009}+\frac{\sqrt{y-2010}-1}{y-2010}+\frac{\sqrt{z-2011}-1}{z-2011}=\frac{3}{4}\)
b) Giải Phương Trình: \(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)
Giúp mình nha.......
a) ĐK: \(x>2009;y>2010;z>2011\)
\(\Leftrightarrow\frac{\sqrt{x-2009}-1}{x-2009}-\frac{1}{4}+\frac{\sqrt{y-2010}-1}{y-2010}-\frac{1}{4}+\frac{\sqrt{z-2011}-1}{z-2011}-\frac{1}{4}=0\)
\(\Leftrightarrow\frac{-\left(\sqrt{x-2009}-2\right)^2}{4\left(x-2009\right)}+\frac{-\left(\sqrt{y-2010}-2\right)^2}{4\left(y-2010\right)}+\frac{-\left(\sqrt{z-2011}-2\right)^2}{4\left(z-2011\right)}=0\left(1\right)\)
Dễ thấy với đkxđ thì \(VT\left(1\right)\le0\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\sqrt{x-2009}=2\\\sqrt{y-2010}=2\\\sqrt{z-2011}=2\end{cases}\Leftrightarrow\hept{\begin{cases}x=2013\\y=2014\\z=2015\end{cases}\left(tm\right)}}\)
\(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)(*)
\(ĐK:\orbr{\begin{cases}x\ge3\\x\le-3\end{cases}}\)
(*)\(\Leftrightarrow\sqrt{\left(x+3\right)\left(x-3\right)}+\sqrt{\left(x-3\right)^2}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\left(tm\right)\\\sqrt{x+3}+\sqrt{x-3}=0\end{cases}}\)
Xét phương trình\(\sqrt{x+3}+\sqrt{x-3}=0\)(**) có \(\sqrt{x+3}\ge0;\sqrt{x-3}\ge0\)nên (**) xảy ra khi \(\hept{\begin{cases}\sqrt{x+3}=0\\\sqrt{x-3}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\x=3\end{cases}}\left(L\right)\)
Vậy phương trình có một nghiệm duy nhất là 3
a. ĐK : x > 2009 ; y > 2010 ; z > 2011
Pt <=> \(\frac{1-\sqrt{x-2009}}{x-2009}+\frac{1-\sqrt{y-2010}}{y-2010}+\frac{1-\sqrt{z-2011}}{z-2011}=-\frac{3}{4}\)
\(\Leftrightarrow\left(\frac{1}{x-2009}-\frac{1}{\sqrt{x-2009}}+\frac{1}{4}\right)+\left(\frac{1}{y-2010}-\frac{1}{\sqrt{y-2010}}+\frac{1}{4}\right)\)
\(\left(\frac{1}{z-2011}-\frac{1}{\sqrt{z-2011}}+\frac{1}{4}\right)=0\)
\(\Leftrightarrow\left(\frac{1}{\sqrt{x-2009}}-\frac{1}{2}\right)^2+\left(\frac{1}{\sqrt{y-2010}}-\frac{1}{2}\right)^2+\left(\frac{1}{\sqrt{z-2011}}-\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(\frac{1}{\sqrt{x-2009}}-\frac{1}{2}\right)^2=0\\\left(\frac{1}{\sqrt{y-2010}}-\frac{1}{2}\right)^2=0\\\left(\frac{1}{\sqrt{z-2011}}-\frac{1}{2}\right)^2=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}\frac{1}{\sqrt{x-2009}}=\frac{1}{2}\\\frac{1}{\sqrt{y-2010}}=\frac{1}{2}\\\frac{1}{\sqrt{z-2011}}=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x-2009}=2\\\sqrt{y-2010}=2\\\sqrt{z-2011}=2\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=2013\\y=2014\\z=2015\end{cases}}\)( tmđk )
b. ĐK : x2 - 9 \(\ge\)0 <=> x2\(\ge\)9 <=> - 3\(\le\)x\(\le\)3
\(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)
\(\Leftrightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+\sqrt{\left(x-3\right)^2}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-3}=0\\\sqrt{x+3}+\sqrt{x-3}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\left(tmdk\right)\\\sqrt{x+3}+\sqrt{x-3}=0\end{cases}}\)
TH :\(\sqrt{x+3}+\sqrt{x-3}=0\)
Vì \(\sqrt{x+3}+\sqrt{x-3}\ge0\forall x\). Dấu "=" xảy ra <=> \(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+3}=0\\\sqrt{x-3}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=3\end{cases}}\)( mâu thuẫn )
Vậy pt có nghiệm duy nhất là x = 3
Giải hệ phương trình sau:
x+y+z+t=14
x+y-z-t=-4
x-y-z+t=0
x-y+z-t=-2
Giải hệ phương trình sau:
x+y+z+t=14
x+y-z-t=-4
x-y-z+t=0
Giải hệ phương trình trên máy tính ta có :
x = 2
y = 3
z = 4
t = 5
Study well
x-y+z-t=-2
Đúng 0
Bình luận (0)