Đặt m =  x 2  – 2x

Ta có:  x 2 - 2 x 2  – 2 x 2  + 4x – 3 = 0

⇔  x 2 - 2 x 2  – 2( x 2  – 2x) – 3 = 0

⇔  m 2 – 2m – 3 = 0

Phương trình  m 2  – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  m 1  = -1,  m 2  = 3

Với m = -1 ta có:  x 2 – 2x = -1 ⇔  x 2  – 2x + 1 = 0

Phương trình  x 2  – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0

Suy ra:  x 1 = x 2  = 1

Với m = 3 ta có:  x 2 – 2x = 3 ⇔  x 2 – 2x – 3 = 0

Phương trình  x 2  – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  x 1  = -1,  x 2 = 3

Vậy phương trình đã cho có 3 nghiệm:  x 1  = 1,  x 2  = -1,  x 3  = 3

\(\Leftrightarrow4\left|x-2\right|=\left(x-2\right)^2+4\)

Đặt \(\left|x-2\right|=t\ge0\)

\(\Rightarrow4t=t^2+4\Rightarrow t^2-4t+4=0\)

\(\Rightarrow\left(t-2\right)^2=0\Rightarrow t=2\)

\(\Rightarrow\left|x-2\right|=2\Rightarrow\left[{}\begin{matrix}x-2=2\\x-2=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)

Mình sẽ k cho bạn nào nhanh nhất nhé <3

\(\frac{1}{x-3}=a,\frac{1}{y-4}=b\)

\(hpt\Leftrightarrow\hept{\begin{cases}a+b=\frac{5}{3}\\4a-3b=\frac{3}{2}\end{cases}\Rightarrow\hept{\begin{cases}a=\frac{13}{14}\\b=\frac{31}{42}\end{cases}\Rightarrow}}\hept{\begin{cases}x=\frac{53}{13}\\y=\frac{166}{31}\end{cases}}\)

Đặt m = 1 / x - 3         và n = 1/y - 4 
Khi đó ta có hệ m + n = 5/3
4 x x - 3 x n = 3/2 
....Bạn tự giải tiếp nhé 

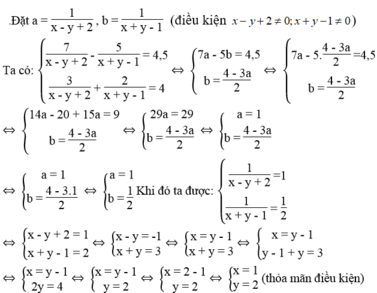
Vậy nghiệm của hệ phương trình là (x; y) = (1; 2).

a) \(x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)

\(\Leftrightarrow-7x^2-9x+4+x^3+3x^2+4x+2=\sqrt[3]{7x^2+9x-4}\)

\(\Leftrightarrow-\left(7x^2+9x-4\right)+\left(x+1\right)^3+x+1=\sqrt[3]{7x^2+9x-4}\) (*)

Đặt \(\sqrt[3]{7x^2+9x-4}=a;x+1=b\)

Khi đó (*) \(\Leftrightarrow-a^3+b^3+b=a\)

\(\Leftrightarrow\left(b-a\right).\left(b^2+ab+a^2+1\right)=0\)

\(\Leftrightarrow b=a\)

Hay \(x+1=\sqrt[3]{7x^2+9x-4}\)

\(\Leftrightarrow\left(x+1\right)^3=7x^2+9x-4\)

\(\Leftrightarrow x^3-4x^2-6x+5=0\)

\(\Leftrightarrow x^3-4x^2-5x-x+5=0\)

\(\Leftrightarrow\left(x-5\right)\left(x^2+x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-1\pm\sqrt{5}}{2}\end{matrix}\right.\)

Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$

$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$

$\Leftrightarrow x-2=0$ hoặc $4-x=0$

$\Leftrightarrow x=2$ hoặc $x=4$ (tm)

Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$

$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$

Với $4x^3-3x^2+6x-4=0(*)$

Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$

Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:

$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$

Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)

Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)

Nãy mình tìm được một cách giải tương tự cho câu 2.

PT \(\Leftrightarrow\left(x-1\right)\left(4x^3-3x^2+6x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x^3-3x^2+6x-4=0\left(1\right)\end{matrix}\right.\)

Vậy pt có 1 nghiệm bằng 1.

\(\left(1\right)\Rightarrow8x^3-6x^2+12x-8=0\)

\(\Leftrightarrow7x^3+x^3-6x^2+12x-8=0\)

\(\Leftrightarrow\left(x-2\right)^3=-7x^3\)

\(\Leftrightarrow x-2=-\sqrt[3]{7}x\)

\(\Leftrightarrow x=\dfrac{2}{1+\sqrt[3]{7}}\)

Vậy pt có nghiệm \(S=\left\{1;\dfrac{2}{1+\sqrt[3]{7}}\right\}\)

Lưu ý: Nghiệm của người kia hoàn toàn tương đồng với nghiệm của mình (\(\dfrac{2}{1+\sqrt[3]{7}}=\dfrac{1}{4}\left(1-\sqrt[3]{7}+\sqrt[3]{49}\right)\))