Góc tạo bởi đường thẳng (d):y=2014(x-1)+2013 và trục Ox là a. Tính tan(180-a)
ko có lời giải ko tick j hết
Những câu hỏi liên quan
Gọi β là góc tạo bởi đường thẳng (d): y = -2016(x - 20152013) + 20142013 và trục Ox.
Khi đó tan(180o - β) = .............
Thì bằng \(-2016\) chứ còn bằng bao nhiêu nữa? Đây là tính chất của hệ số góc mà.
Đúng 0
Bình luận (0)
gọi a là góc tạo bởi đường thẳng =-6x+ và trục Ox. Khi đó tan(180 độ-a) bằng bao nhiêu
giúp mình với m.n cần gấp
cho y=2x+5 (d)
a) Điểm M (3;3) và N (6;17) có nằm trên đường thẳng (d) ko
b) tính góc tạo bởi đường thẳng (d') với trục ox. Biết d' // d
cho đường thẳng y(5-2m)x+m+2 (d)a) Tìm m để đường thẳng (d) đi qua A(dfrac{1}{2};2)b) Tìm m để đường thẳng (d) tạo bởi trục Ox, góc nhọn góc tù.c) Vẽ đường thẳng (d) với m2. Tính góc tạo đường thẳng với trục Oxd) Gọi M,N lần lượt là giao điểm của đường thẳng (d) với trục Ox.Tìm m để SOMNdfrac{1}{2}
Đọc tiếp
cho đường thẳng y=(5-2m)x+m+2 (d)
a) Tìm m để đường thẳng (d) đi qua A(\(\dfrac{1}{2}\);2)
b) Tìm m để đường thẳng (d) tạo bởi trục Ox, góc nhọn góc tù.
c) Vẽ đường thẳng (d) với m=2. Tính góc tạo đường thẳng với trục Ox
d) Gọi M,N lần lượt là giao điểm của đường thẳng (d) với trục Ox.Tìm m để SOMN=\(\dfrac{1}{2}\)
Cho hai đường thẳng y – x + 3 ( d) và y x – 1 . (d) a) Tìm tọa độ giao điểm M của d và d. b) Vẽ d và d trên cùng một hệ trục tọa độ. c) Tính góc tạo bởi đường thẳng (d) và (d’) với trục Ox d) Đường thẳng d cắt Ox tại A và Oy tại B; d cắt Ox tại C và Oy tại D. Tính diện tích tam giác BMD. e) Tìm m để đường thẳng (d’’) y mx + m + 2 và đường thẳng (d) và (d’) đồng quy
Đọc tiếp
Cho hai đường thẳng y = – x + 3 ( d) và y = x – 1 . (d') a) Tìm tọa độ giao điểm M của d và d'. b) Vẽ d và d' trên cùng một hệ trục tọa độ. c) Tính góc tạo bởi đường thẳng (d) và (d’) với trục Ox d) Đường thẳng d cắt Ox tại A và Oy tại B; d' cắt Ox tại C và Oy tại D. Tính diện tích tam giác BMD. e) Tìm m để đường thẳng (d’’) y = mx + m + 2 và đường thẳng (d) và (d’) đồng quy
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
gọi a là góc tạo bởi đường thẳng y=2x-3 và trục ox khi đó tan a bằng
cậu lúc nào cung '' a '' vậy oOo KiRitO oOo
Đúng 0
Bình luận (0)
Trong hệ trục tạo độ Oxy có đường thẳng (d) y = 2014 - x cắt Ox tại A và Oy tại B Điểm M di chuyển trên AB ( M ko trùng A,B)
Tìm Min \(P=\frac{x}{\sqrt{2014-x}}+\frac{y}{\sqrt{2014-y}}\)
Bài 1: Cho hàm số : y x −3 có đồ thị là đường thẳng (d) 1
a/ Tính giá trị hàm số khi x0; x−3x 1/3
b/ Tìm giá trị của biến số x khi y0;y-7^3
c/ Xác định hệ số góc của đường thẳng d . Góc tạo bởi d và trục Ox là góc nhọn hay tù?
d/. Cho biết tọa độ các giao điểm A,B của đồ thị với trục tung và trục hoành .
e/ Vẽ đồ thị hàm số g/ Tính OA;OB và AB.
Đọc tiếp
Bài 1: Cho hàm số : y = x −3 có đồ thị là đường thẳng (d) 1
a/ Tính giá trị hàm số khi x=0; x=−3x= 1/3
b/ Tìm giá trị của biến số x khi y=0;y=-7^3
c/ Xác định hệ số góc của đường thẳng d . Góc tạo bởi d và trục Ox là góc nhọn hay tù?
d/. Cho biết tọa độ các giao điểm A,B của đồ thị với trục tung và trục hoành .
e/ Vẽ đồ thị hàm số g/ Tính OA;OB và AB.
13 tháng 12 2023 lúc 16:44
Cho 2 đường thẳng (d₁): y dfrac{1}{2}x+2 (d₂): y -x+2 a) Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ Oxy.b) Tính góc tạo bởi (d₁) và trục Ox.c) Gọi A và B lần lượt là giao điểm của (d₁) và (d₂) với trục Ox, C là giao điểm của (d₁) và (d₂). Tính chu vi và diện tích ∆ABC (đơn vị trên hệ trục tọa độ là cm)
Đọc tiếp
Cho 2 đường thẳng
(d₁): y = \(\dfrac{1}{2}x+2\)
(d₂): y = \(-x+2\)
a) Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ Oxy.
b) Tính góc tạo bởi (d₁) và trục Ox.
c) Gọi A và B lần lượt là giao điểm của (d₁) và (d₂) với trục Ox, C là giao điểm của (d₁) và (d₂). Tính chu vi và diện tích ∆ABC (đơn vị trên hệ trục tọa độ là cm)
a:
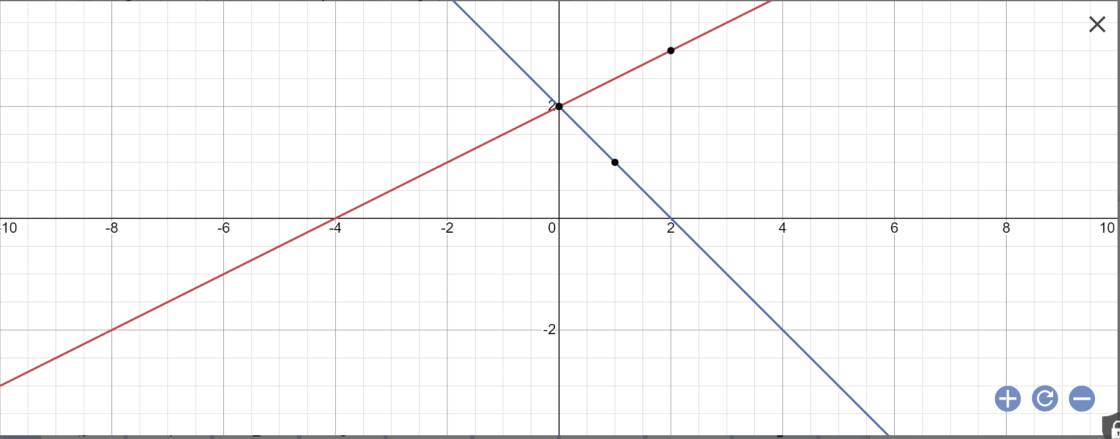
b: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
(d1): \(y=\dfrac{1}{2}x+2\)
=>\(a=\dfrac{1}{2}\)
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-2\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x+2=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=0\\y=-x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)
Vậy: A(-4;0); B(2;0); C(0;2)
\(AB=\sqrt{\left(2+4\right)^2+\left(0-0\right)^2}=6\)
\(AC=\sqrt{\left(0+4\right)^2+\left(2-0\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=6+2\sqrt{5}+2\sqrt{2}\)(cm)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{36+20-8}{2\cdot6\cdot2\sqrt{5}}=\dfrac{48}{24\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{1}{\sqrt{5}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot6\cdot2\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=6\)
Đúng 2
Bình luận (0)