Số đo tính theo đơn vị rađian của góc 135 ° là:
A. 2 π 3
B. 3 π 4
C. 5 π 6
D. 6 π 7
Những câu hỏi liên quan
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
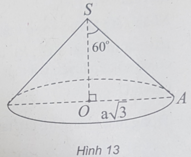
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với biên độ A, tần số góc ω. Chọn gốc thời gian lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động của vật là: A. x= Acos(ωt+π/4) B. x= Acos(ωt-π/2) C. x= Acos(ωt+π/2) D. x= Acos(ωt) [Cho mik lời giải chi tiết vs ạ]
Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B
Đúng 1
Bình luận (0)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π/2 α π, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung
A
M
3
là A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
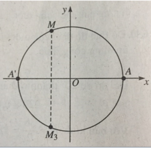
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo pt x=6cosωt(cm) (t đo bằng s). Quãng đường ngắn nhất để vật đi từ vị trí có pha bằng π/2rad đến vị trí có pha -π/3 rad là
Bài 1: Ba đơn vị vận tải cùng góp 54 triệu để xây một cây cầu. Tính số tiền mỗi đơn vị góp, biết rằng số tiền góp tỉ lệ thuận với khoảng cách (đơn vị 1 cách cầu 2km; đơn vị 2 cách cầu 5 km; đơn vị 3 cách cầu 8km)Bài 2 : Tìm số đo ba góc của tam giác ABC, biết:a/ Số đo ba góc tỉ lệ với 2; 3; 4.b/ Số đo của góc A bằng 3 lần số đo của góc B; số đo của góc B bằng 2 lần số đo của góc C.
Đọc tiếp
Bài 1: Ba đơn vị vận tải cùng góp 54 triệu để xây một cây cầu. Tính số tiền mỗi đơn vị góp, biết rằng số tiền góp tỉ lệ thuận với khoảng cách (đơn vị 1 cách cầu 2km; đơn vị 2 cách cầu 5 km; đơn vị 3 cách cầu 8km)
Bài 2 :
Tìm số đo ba góc của tam giác ABC, biết:
a/ Số đo ba góc tỉ lệ với 2; 3; 4.
b/ Số đo của góc A bằng 3 lần số đo của góc B; số đo của góc B bằng 2 lần số đo của góc C.
Bài 3: Một con lắc đơn có chiều dài dây treo 1 m, dao động điều hòa tại nơi có gia tốc trọng trường g π2 m/s2.Số lần động năng bằng thế năng trong khoảng thời gian 4 s là A. 16. B. 6. C. 4. D. 8.Bài 4: Một vật dao động điều hoà theo phương trình x 2cos(5πt -π/3) (cm) (t đo bằng giây).Trong khoảng thời gian từ t 1 (s) đến t 2 (s) vật đi qua vị trí x 0 cm được mấy lần? A. 6 lần. B. 5 lần. C. 4 lần. D. 7 lần. Bài 5: Một chất điểm dao động điều hòa theo phương trình x Acos(2πt/T + π/4) (cm). Tr...
Đọc tiếp
Bài 3: Một con lắc đơn có chiều dài dây treo 1 m, dao động điều hòa tại nơi có gia tốc trọng trường g π2 m/s2.
Số lần động năng bằng thế năng trong khoảng thời gian 4 s là A. 16. B. 6. C. 4. D. 8.
Bài 4: Một vật dao động điều hoà theo phương trình x = 2cos(5πt -π/3) (cm) (t đo bằng giây).
Trong khoảng thời gian từ t = 1 (s) đến t = 2 (s) vật đi qua vị trí x = 0 cm được mấy lần? A. 6 lần. B. 5 lần. C. 4 lần. D. 7 lần. Bài 5: Một chất điểm dao động điều hòa theo phương trình x = Acos(2πt/T + π/4) (cm). Trong khoảng thời gian 2,5T đầu tiên từ thời điểm t = 0, chất điểm đi qua vị trí có li độ x = 2A/3 là A. 9 lần. B. 6 lần. C. 4 lần. D. 5 lần.
Bài 6: Một chất điểm dao động điều hoà có vận tốc bằng không tại hai thời điểm liên tiếp là t1 = 2,2 (s) và t2 = 2,9 (s). Tính từ thời điểm ban đầu (to = 0 s) đến thời điểm t2 chất điểm đã đi qua vị trí cân bằng A. 9 lần. B. 6 lần. C. 4 lần. D. 5 lần
. Bài 7: Một vật dao động điều hoà theo phương trình: x = 2cos(5πt - π/3) (cm). Trong giây đầu tiên kể từ lúc bắt đầu dao động vật đi qua vị trí có li độ x = -1 cm theo chiều dương được mấy lần? A. 2 lần. B. 3 lần. C. 4 lần. D. 5 lần.
Bài 8: Một chất điểm dao động điều hoà tuân theo quy luật: x = 5cos(5πt - π/3) (cm). Trong khoảng thời gian t = 2,75T (T là chu kì dao động) chất điểm đi qua vị trí cân bằng của nó A. 3 lần. B. 4 lần. C. 5 lần. D. 6 lần.
Bài 9: Một chất điểm dao động điều hòa với phương trình: x = 4cos(4πt + π/3) (cm). Trong thời gian 1,25 s tính từ thời điểm t = 0, vật đi qua vị trí có li độ x = -1 cm A. 3 lần. B. 4 lần. C. 5 lần. D. 6 lần. Bài 10: Chất điểm dao động điều hòa với phương trình: x = Acos(2πt/T + π/4) (cm). Trong thời gian 2,5T kể từ thời điểm t = 0, số lần vật đi qua li độ x = 2A/3 làπ A. 6 lần. B. 4 lần. C. 5 lần. D. 9 lần.
Xét một vecto quay OM→ có những đặc điểm sau: - Có độ lớn bằng hai đơn vị chiều dài. - Quay quanh O với tốc độ góc 1 rad/s - Tại thời điểm t 0, vecto OM→ hợp với trục Ox một góc 30o Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào? A. x 2cos(t – π/3) B. x 2cos(t + π/6) C. x 2cos(t - 30o) D. x 2cos(t + π/3)
Đọc tiếp
Xét một vecto quay OM→ có những đặc điểm sau:
- Có độ lớn bằng hai đơn vị chiều dài.
- Quay quanh O với tốc độ góc 1 rad/s
- Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o
Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – π/3) B. x = 2cos(t + π/6)
C. x = 2cos(t - 30o) D. x = 2cos(t + π/3)
Chọn đáp án B.
Vecto quay OM→ có:
+ Có độ lớn bằng hai đơn vị chiều dài nên biên độ dao động A = 2.
+ Quay quanh O với tốc độ góc 1 rad/s nên tần số ω = 1rad/s.
+ Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 rad.
Phương trình dao động: x = 2.cos(t + π/6).
Đúng 0
Bình luận (0)
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
Một nguồn sóng o dao động theo phương trình
u
0
(t) Acos100
π
t. Sóng truyền từ o đến M cách nó 30 cm với tốc độ 10 m/s. Phương trình dao động của M làA.
u
M
(t) Acos(100
π
t + 3
π
/2)B.
u
M
(t) Acos100
π...
Đọc tiếp
Một nguồn sóng o dao động theo phương trình u 0 (t) = Acos100 π t. Sóng truyền từ o đến M cách nó 30 cm với tốc độ 10 m/s. Phương trình dao động của M là
A. u M (t) = Acos(100 π t + 3 π /2)
B. u M (t) = Acos100 π t.
C. u M (t) = Acos(100 π t - 3 π )
D. u M (t) = Acos(100 π t + π )