bài này ez mà :D ( Tự vẽ hình ) Vì EF // AB nên ta có thể viết như sau: 

\(\overrightarrow{AB}.\overrightarrow{EG}=\overrightarrow{EF}.\overrightarrow{EG}=\overrightarrow{EF}\left(\overrightarrow{EF}+\overrightarrow{FG}\right)=EF^2+\overrightarrow{EF}.\overrightarrow{FG}=a^2\)

( Vì: \(\overrightarrow{EF}.\overrightarrow{FG}=\left|\overrightarrow{EF}\right|.\left|\overrightarrow{FG}\right|.\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=0\)) ( \(\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=90^0=0\)) 

Đáp án : C

Chọn C

Đáp án là A.

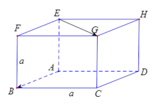
Ta có:  

A B → . E G → = A B . E G . cos A B → ; E G → ^ = A B . A C . cos B A C ^ = a 2 2 . 2 2 = a 2 .

a. Gọi cạnh lập phương là a

Ta có: \(AC=\sqrt{AB^2+AD^2}=a\sqrt{2}\) 

\(AH=\sqrt{AD^2+DH^2}=a\sqrt{2}\)

\(CH=\sqrt{CD^2+DH^2}=a\sqrt{2}\)

\(\Rightarrow\Delta ACH\) đều \(\Rightarrow\widehat{CAH}=60^0\)

b.

Do \(B'C||A'D\Rightarrow\) góc giữa A'B và B'C bằng góc giữa A'B và A'D

Tương tự câu a, ta có tam giác A'BD đều \(\Rightarrow\widehat{BA'D}=60^0\)

c.

Do IJ song song SB (đường trung bình), CD song song AB \(\Rightarrow\) góc giữa IJ và CD bằng góc giữa SB và AB

Tam giác SAB đều (các cạnh bằng a) \(\Rightarrow\widehat{SBA}=60^0\)

d.

\(\overrightarrow{EG}=\overrightarrow{AC}\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}=60^0}\) do tam giác FAC đều 

1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)

Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều

\(\Rightarrow\widehat{FAC}=60^0\)

2.

Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC

\(\Rightarrow IJ||SB\)

Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)

c

C

c