Tìm tất cả các giá trị thực của tham số m để phương trình log 2 cos x - m log cos 2 x - m 2 +4 = 0
vô nghiệm.
![]()
![]()
![]()
![]()
Tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m - 1 cos x - m + 1 = 0 có đúng 2 nghiệm thuộc đoạn - π 2 ; π 2 là
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1
C. - 1 ≤ m ≤ 1
D. 0 ≤ m ≤ 1
Tìm tất cả các giá trị của tham số m để phương trình cos 4 x = cos 2 3 x + m . sin 2 x có nghiệm x ∈ 0 , π 12
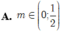
![]()
![]()
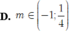
Tìm tất cả các giá trị của tham số m để phương trình log2 (|cos x|) – 2mlog(cos2 x) – m2 + 4 = 0 vô nghiệm?
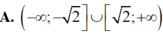
![]()

![]()
Đáp án C
Ta có : PT <=> log2 |cos x| – 2mlog|cos x| – m2 + 4 = 0
Đặt t = log|cos x|; t ∈ ( - ∞ ; 0 ]
Khi đó: t2 – 2mt – m2 + 4 = 0 (*)
PT đã cho vô nghiệm <= > (*) vô nghiệm hoặc có nghiệm dương.

Cho phương trình log 2 x = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực.
A. m ≥ 0
B. m ∈ ℝ
C. m > 0
D. m ∈ ℤ
Đáp án là B
Tập giá trị của hàm số log a x = R
Cho phương trình log 2 m = m với x > 0. Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thực
A. m ≥ 0
B. m ∈ R
C. m > 0
D. < 0
Tất cả các giá trị của tham số m để phương trình log m x = 2 log x + 1 có nghiệm là
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Đáp án C
Phương pháp:

![]() phương trình trở thành
phương trình trở thành
![]()
![]()
![]()
=> Hàm số đồng biến trên khoảng [2;+∞)
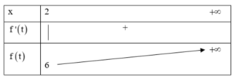
Để phương trình (*) có nghiệm thì 2m ≥ 6 ⇔ m ≥ 3
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥1?
A. m ϵ [2;+∞).
B. m ϵ [3;+∞).
C. m ϵ (-∞;2].
D. m ϵ (-∞;3].
Tìm tất cả các giá trị thực của tham số m để bất phương trình -2x2 +2(m-2)x+m-2<0 có nghiệm