Tìm các số thực x, y sao cho: (1 - 2i)x + (1 + 2i)y = 1 + i
A. x = 1 4 , y = 3 4
B. x = 1 4 , y = - 3 4
C. x = - 1 4 , y = 3 4
D. x = - 1 4 , y = - 3 4
Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
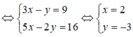
Vậy: T = |x - y| = 5
Tìm các số thực x, y sao cho ( x – 2 y ) + ( x + y + 4 ) . i = ( 2 x + y ) + 2 y i .
A. x = 3, y = 1
B. x = 3, y = -1
C. x = -3, y = -1
D. x = -3, y = 1
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
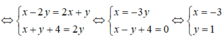
Vậy x = -3, y = 1.
Chọn đáp án D.
1:Tìm GTNN x^2+y^2 biết :(x^2-y^2+1)+4x^2y^2-x^2-y^2=0
2:Cho a nhỏ hơn hoặc =a,b,c nhỏ hơn hoặc =1.Tìm GTNN,GTLN của biểu thức:P=a+b+c-ab-bc-ca
3:cho các số thực nguyên thỏa mãn điều kiện :x^2+y^2+z^2 nhỏ hơn hoặc = 27.Tìm giá trị nhỏ nhất ,GTLN x+y+z+xy+yz+zx
4: cho x,y dương thỏa mãn dk: x+y=1.Tìm GTNN:M=(x+1/x)+(y+1/y)
Bài 1:Cho a,b là các số nguyên tố thỏa mãn: (a-1) chia hết cho b và (b3 - 1) chia hết cho a.Chứng minh: a= b2+b+1
Bài 2:Cho x,y là hai số thực thỏa mãn:
x3 + y3 +3x2 + 4x + 3y2 +4y +4=0.Tìm giá trị lớn nhất của biểu thức P=1/x+1/y
1) Vì a, b là số nguyên tố và a - 1 chia hết cho b nên a là số nguyên tố lẻ >=3 và b =2( vì a -1 chẵn)
b3 - 1 = 7 chia hết cho a, nên a =7. Vậy a = b2 + b + 1( 7 = 22 + 2 + 1)
TÌM x, y, z, thuộc Q biết:
a,I x+1/2I+I y-3/4I+I z+1I=0
\(\left|x+\frac{1}{2}\right|+\left|y-\frac{3}{4}\right|+\left|z+1\right|=0\)
\(\Rightarrow\hept{\begin{cases}\left|x+\frac{1}{2}\right|=0\\\left|y-\frac{3}{4}\right|=0\\\left|z+1\right|=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=0-\frac{1}{2}\\y=0+\frac{3}{4}\\z=0-1\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{-1}{2}\\y=\frac{3}{4}\\z=-1\end{cases}}\)
Tìm các số thực x,y,z thỏa mãn (x−1)^2 +|3y−1|+|z+2| = 0.
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\left|3y-1\right|\ge0\forall y\)
\(\left|z+2\right|\ge0\forall z\)
Do đó: \(\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left(x,y,z\right)=\left(1;\dfrac{1}{3};-2\right)\)
Tìm các cặp số nguyên x , y sao cho
A, x . y = -10
B, ( 2 . x - 1 ) . ( x + 4 ) = 11
cậu b cũng tương tự
vd:11=1.11=11.1=(-11).(-1)=(-1)/(-11)
Suy ra:
| 2x-1 | 1 | 11 | -11 | -1 |
| x+4 | 11 | 1 | -1 | -11 |
rồi bạn tìm x thôi
cho x,y là các số thực ko âm t/m: x+y+z=2.Tìm giá trị nhỏ nhất của biểu thức:P= x^4+Y^4+Z^4
Bài tập số 3: Tìm các số thực x,y thỏa mãn.
a, (3 - 2i) x + (5 - 7i) y = 1 - 3i
b, \(\left(1+2i\right)^2x-\left(4-5i\right)y=2i\)
Lời giải:
a)
$(3-2i)x+(5-7i)y=1-3i$
$\Leftrightarrow (3x+5y)-(2x+7y)i=1-3i$
\(\Leftrightarrow \left\{\begin{matrix}
3x+5y=1\\
2x+7y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\frac{-8}{11}\\
y=\frac{7}{11}\end{matrix}\right.\)
b)
\((1+2i)^2x-(4-5i)y=2i\)
\(\Leftrightarrow (-3+4i)x-(4-5i)y=2i\)
\(\Leftrightarrow -(3x+4y)+(4x+5y)i=2i\Leftrightarrow \left\{\begin{matrix} -(3x+4y)=2\\ 4x+5y=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=10\\ y=-8\end{matrix}\right.\)