Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.
A. tan α = sin α cos α
B. c o t α = cos α sin α
C. tan α . co t α = 1
D. tan 2 α - 1 = cos 2 α
Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.
A. tan α = sin α cos α
B. c o t α = cos α sin α
C. tan α . c o t α = 1
D. tan 2 α - 1 = cos 2 α
Đáp án D
Cho α là góc nhọn bất kỳ, khi đó
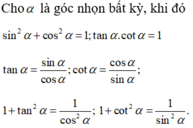
Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90 ° . Chọn khẳng định đúng.
A. α + β = 90 °
B. tan α = cot β
C. tan α = cos α
D. tan α = tan β
Đáp án B
Với hai góc α và β mà α + β = 90 °
sin α = cos β ; cos α = sin β
tan α = cot β ; cot α = tan β
Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90 ° . Chọn khẳng định đúng.
A. tan α = sin β
B. tan α = cot β
C. tan α = cos α
D. tan α = tan β
Đáp án B
Với hai góc α và β mà α + β = 90 °
sin α = cos β ; cos α = sin β
tan α = cot β ; cot α = tan β
Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.
A. sin α + cos α = 1
B. sin 2 α + cos 2 α = 1
C. sin 3 α + cos 3 α = 1
D. sin α - cos α = 1
Đáp án B
Cho α là góc nhọn bất kỳ, khi đó sin 2 α + cos 2 α = 1
Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.
A. sin α + cos α = 1
B. sin 2 α + cos 2 α = 1
C. sin 3 α + cos 3 α = 1
D. sin α - cos α = 1
Đáp án B
Cho α là góc nhọn bất kỳ, khi đó sin 2 α + cos 2 α = 1
Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.
A. sin α + cos α = 1
B. sin2 α + cos2 α = 1
C. sin3 α + cos3 α = 1
D. sin α − cos α = 1
Cho α là góc nhọn bất kỳ. Khi đó sin2 α + cos2 α = 1
Đáp án cần chọn là: B
Cho góc nhọn α. Biết sin α · cos α = 12 / 25 , tính sin α, cos α, tan α.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được
Cho góc nhọn α có cot α = 2/3 . Tính sin α, cos α, tan α
Cho góc nhọn α, biết cos α = \(\dfrac{1}{5}\). Tính sin α, tan α, cot α.
\(sin\alpha^2+cos\alpha^2=1\Rightarrow sin\alpha^2=1-cos\alpha^2=1-\dfrac{1}{25}=\dfrac{24}{25}\Rightarrow sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\Rightarrow cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\sin^2\alpha=1-\dfrac{1}{25}=\dfrac{24}{25}\)
hay \(\sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{2\sqrt{6}}{5}:\dfrac{1}{5}=2\sqrt{6}\)
\(\cot\alpha=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)