A. BC // mp(AA’B’B)
B. BC // mp(A’B’C’D’)
C. BC // mp(ABCD)
D. BC // mp(DCC’D’)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
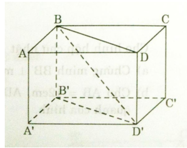
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
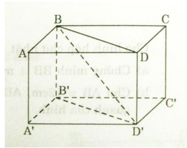
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Hình thang ABCD (AB//CD) có M, N, P, Q thứ tự là trung điểm của AB, BC, CD, DA. Khẳng định nào sau đây đúng
A. MP // BC B. MP // BC và MP=
C. NQ = D. NQ //AB và NQ =
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD.
a) Cmr: CD vuông góc mp (SAD)
b) Cmr: (SAC) vuông góc mp (SBD)
c) Tính góc giữa SC v à mp (ABCD)
d) Tính góc giữa mp ( SAB) và mp (SBC).
e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Cho tứ giác ABCD có M,N,P,Q lần lượt là trung điểm của AB,BC,CD,AD.CMR:
a) MP nhỏ hơn hoặc bằng (AD+BC)/2
b) ABCD là hình thang nếu MP+NQ=(AB+AD+BC+CD)/2
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại A và B, Kẻ \(SA\) vuông góc với \(mp\left(ABCD\right)\). Biết rằng \(AB=BC=a\), \(AD=2a\) góc giữa \(SB\) và \(mp\left(ABCD\right)\) bằng \(45^0\)
a) Chứng minh rằng BC vuông góc với SB, và \(mp\left(SCD\right)\perp mp\left(SAC\right)\)
b) Gọi \(mp\left(\alpha\right)\) là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp \(S.ABCD\) và \(mp\left(\alpha\right)\). Tính diện tích của thiết diện đó theo \(a\).
P/s: Em xin nhờ quý thầy cô giáo và các bạn yêu toán trên toàn quốc giúp em ý b với ạ
Em cám ơn nhiều lắm ạ!
Cho tứ giác ABCD có \(\widehat{B}=\widehat{D}=90^0\). Từ M trên AC kẻ MN⊥BC;MP⊥AD(N∈BC;P∈AD)
a) Chứng minh \(\frac{MN}{BC}+\frac{MP}{AD}=1\)
Ta có MN vuông góc BC (gt)
AB vuông góc BC (gt)
=> MN // AB
Theo đinh lí Talet ta được \(\frac{MN}{AB}=\frac{CN}{BC}=\frac{CM}{AC}\) (1)
Ta có MP vuông góc AD (gt)
DC vuông góc AD (gt)
=> MP // DC
Theo đinh lí Talet ta được \(\frac{MP}{DC}=\frac{AP}{AD}=\frac{AM}{AC}\) (2)
Từ (1) và (2) => \(\frac{MN}{BC}+\frac{MP}{AD}=\frac{CM}{AC}+\frac{AM}{AC}=\frac{CM+AM}{AC}=\frac{AC}{AC}=1\)(ĐPCM)
Wi ơi. Theo bạn đề bài đúng bay sai? Mik suy nghĩ một tuần rồi mà vẫn k lm giống đề đc , mik chỉ lm đc như Wi lm thoyy
๖ۣۜIňǫśǖƙɛ☣๖ۣۜHašђïƀĭrä¹⁶་⁰⁷༄༂ℑøáη•ℌọς༂
mik đâu thấy sai ở chổ nào ạ???, hình abcd dù có d và b vuông thì vx là tứ giác mà???
cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB =2a, BC=3a/2, AD=3a. Hình chiếu vuông góc của S lên mp (ABCD) là trung điểm H của BD. Biết góc giữa mp (SCD) và mp (ABCD) bằng 60 . Tính khoảng cách
a> từ C đến mp (SBD)
b> từ B đến mp (SAH)
giúp mình tính kết quả là bn với ạ..