Cho a > b > 0. So sánh a2 và ab; a3 và b3?
A. a2 < ab và a3 > b3.
B. a2 > ab và a3 > b3.
C. a2 < ab và a3 < b3
D. a2 > ab và a3 < b3
Với a, b, c bất kỳ. Hãy so sánh a2 + b2 + c2 và ab + bc + ca?
A. a2 + b2 + c2 = ab + bc + ca
B. a2 + b2 + c2 ≥ ab + bc + ca
C. a2 + b2 + c2 ≤ ab + bc + ca
D. a2 + b2 + c2 > ab + bc + ca
Xét hiệu:
a2 + b2 + c2 - ab - bc - ca
= 1 2 (2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca)
= 1 2 [(a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2)]
= 1 2 [(a - b)2 + (b - c)2 + (c - a)2] ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c)
Nên a2 + b2 + c2 ≥ ab + bc + ca.
Dấu “=” xảy ra khi a = b = c.
Đáp án cần chọn là: B
Cho hình vẽ bên biết a // b và A 1 ^ + A 2 ^ + A 3 ^ = 310 ° .
a) Tính A 1 ^
b) So sánh A 2 ^ và B 4 ^

a) Ta có: A 1 ^ + A 2 ^ + A 3 ^ = 310 ° mà A 2 ^ + A 3 ^ = 180 ° ( hai góc kề bù)
do đó A 1 ^ = 310 ° − 180 ° = 130 ° .
b) Ta có: B 2 ^ = A 2 ^ (hai góc đồng vị); B 2 ^ = B 4 ^ (hai góc đối đỉnh).
Suy ra A 2 ^ = B 4 ^
cho ba so a,b,c khac 0 thoa man ab+bc +ac = 0 .tinh B=bc/a2 + ca/b2 + ab/c2
\(ab+bc+ca=0\)
=> \(\frac{ab+bc+ca}{abc}=0\)
=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
Đặt: \(\frac{1}{a}=x;\)\(\frac{1}{b}=y;\)\(\frac{1}{c}=z\)
Ta có: \(x+y+z=0\)
=> \(x^3+y^3+z^3=3xyz\) (tự c/m, ko c/m đc ib)
hay \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(B=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc.\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)
\(=abc.\frac{3}{abc}=3\)
Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: a 2 < ab và ab < b 2
Với a > 0, b > 0 ta có:
a < b ⇒ a.a < a.b ⇒ a 2 < ab (1)
a < b ⇒ a.b < b.b ⇒ ab < b 2 (2)
a) Cho phân số a b ( a , b ∈ ℕ , b ≠ 0 ) .Giả sử a b <1 và m ∈ ℕ , m ≠ 0 . Chứng tỏ rằng a b < a + m b + m .
b) Áp dụng so sánh: 437 564 v à 446 573 .
a) Thực hiện quy đồng a b = a ( b + m ) b ( b + m ) = a b + a m b 2 + b m ;
a + m b + m = b ( a + m ) b ( b + m ) = a b + b m b 2 + b m . Vì a b < 1=> a < b => ab +am < ab + bm
Từ đó thu được a b < a + m b + m
b) 437 564 < 437 + 9 564 + 9 = 446 573 .
1, Cho a,b,n thuộc Z ; b>0 ; n>0 . So sánh: $\frac{a}{b}$ab và $\frac{a+n}{b+n}$a+nb+n
2, Cho a1 < a2 < ........ < a9. Chứng minh rằng: $\frac{a_1+a_2+...+a_9}{a_3+a_6+a_9}$a1+a2+...+a9a3+a6+a9 < 3
Cho a, b ∈ Z, b > 0. So sánh 2 số hữu tỉ a b v à a + 2001 b + 2001
Ta có: a(b+ 2001) = ab + 2001a
b(a+ 2001) = ab + 2001b
Vì b > 0 nên b + 2001 > 0
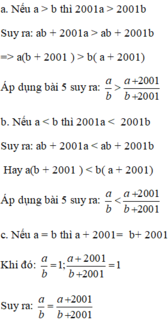
Với a, b, c bất kỳ. Hãy so sánh 3(a2 + b2 + c2) và (a + b + c)2
A. 3(a2 + b2 + c2) = (a + b + c)2
B. 3(a2 + b2 + c2) ≤ (a + b + c)2
C. 3(a2 + b2 + c2) ≥ (a + b + c)2
D. 3(a2 + b2 + c2) < (a + b + c)2
Xét hiệu:
3(a2 + b2 + c2) - (a + b + c)2
= 3a2 + 3b2 + 3c2 - a2 - b2 - c2 - 2ab - 2bc - 2ac
= 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac
= (a - b)2 + (b - c)2 + (c - a)2 ≥ 0
(vì (a - b)2 ≥ 0; (b - c)2 ≥ 0; (c - a)2 ≥ 0 với mọi a, b, c
Nên 3(a2 + b2 + c2) ≥ (a + b + c)2.
Đáp án cần chọn là: C
Cho a>b>0 và a-b=7 và ab=60. Không tính a,b hãy tính a2-b2 và a4+b4
\(a>b>0\Rightarrow a+b>0\)
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab=7^2+4.60=289\Rightarrow a+b=17\)
\(\Rightarrow a^2-b^2=\left(a-b\right)\left(a+b\right)=7.17=119\)
\(a^2+b^2=\left(a-b\right)^2+2ab=7^2+2.60=169\)
\(\Rightarrow a^4+b^4=\left(a^2+b^2\right)^2-2\left(ab\right)^2=169^2-2.60^2=21361\)