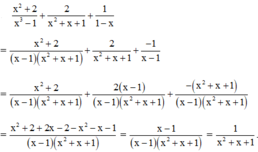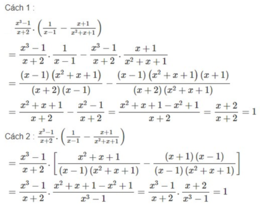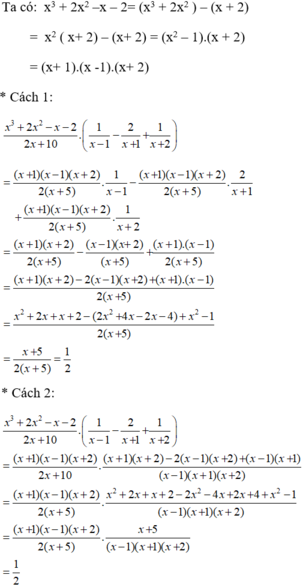Thực hiện phép cộng: 1 1 - x + 1 1 + x + 2 1 + x 2 + 4 1 + x 2 + 8 1 + x 2 + 16 1 + x 2
Những câu hỏi liên quan
Thực hiện phép cộng các phân thức sau
4
x
2
-
3
x
+
17
x
3
-
1
+
2
x
-
1
x
2...
Đọc tiếp
Thực hiện phép cộng các phân thức sau 4 x 2 - 3 x + 17 x 3 - 1 + 2 x - 1 x 2 + x + 1 + 6 1 - x
Ta có:
+
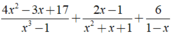
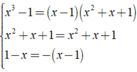⇒ MTC = - ( x - 1 )( x2 + x + 1 )
Khi đó ta có:
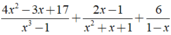
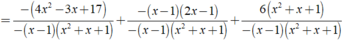
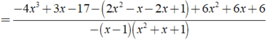
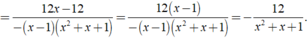
Đúng 0
Bình luận (0)
Thực hiện phép cộng các phân thức sau:
4
x
2
-
3
x
+
17
x
3
-
1
+
2
x
-
1
x
2
+
x
+...
Đọc tiếp
Thực hiện phép cộng các phân thức sau: 4 x 2 - 3 x + 17 x 3 - 1 + 2 x - 1 x 2 + x + 1 + 6 1 - x
Ta có: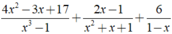
+
⇒
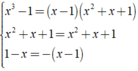M
T
C
=
-
(
x
-
1
)
(
x
2
+
x
+
1
)
Khi đó ta có:
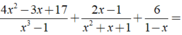
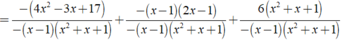
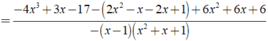
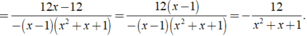
Đúng 0
Bình luận (0)
Thực hiện phép cộng các phân thức sau: x+1/ 2x+6 + 2x+3 / x(x+3)
Ta có: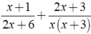
+
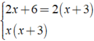⇒ MTC = 2x( x + 3 )
Khi đó ta có:
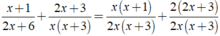
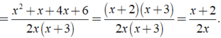
Đúng 0
Bình luận (0)
Dùng quy tắc đổi dấu để tìm mẫu thức chung rồi thực hiện phép cộng:
x
2
+
2
x
3
-
1
+
2
x
2
+
x
+
1
+
1
1
-
x
Đọc tiếp
Dùng quy tắc đổi dấu để tìm mẫu thức chung rồi thực hiện phép cộng: x 2 + 2 x 3 - 1 + 2 x 2 + x + 1 + 1 1 - x
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
-
1
x
+
2
.
1
x
-
1
-...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 - 1 x + 2 . 1 x - 1 - x + 1 x 2 + x + 1
Thực hiện phép cộng sau: P= \(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}\)
Mọi người giúp em vs ạ! Em cần gấp
Thực hiện phép cộng :
\(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(A=\left(\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{1-x}{\left(1+x\right)\left(1-x\right)}\right)+...+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{1+x+1-x}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
Tiếp tục các bước như ở dòng 2 và 3 ta có :
\(A=\dfrac{16}{1-x^{16}}+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{16\left(1+x^{16}\right)}{\left(1-x^{16}\right)\left(1+x^{16}\right)}+\dfrac{16\left(1-x^{16}\right)}{\left(1+x^{16}\right)\left(1-x^{16}\right)}\)
\(A=\dfrac{16+16x^{16}+16-16x^{16}}{1-x^{32}}\)
\(A=\dfrac{32}{1-x^{32}}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
+
2
x
2
-
x
-
2
2
x
+
10
.
1
x...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 + 2 x 2 - x - 2 2 x + 10 . 1 x - 1 - 2 x + 1 + 1 x + 2
thực hiện phép cộng có số tu nhiên vơi 1 vơi 1 27,58
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:25
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{1}{{2a}} + \dfrac{2}{{3b}}\)
b) \(\dfrac{{x - 1}}{{x + 1}} - \dfrac{{x + 1}}{{x - 1}}\)
c) \(\dfrac{{x + y}}{{xy}} - \dfrac{{y + z}}{{yz}}\)
d) \(\dfrac{2}{{x - 3}} - \dfrac{{12}}{{{x^2} - 9}}\)
e) \(\dfrac{1}{{x - 2}} + \dfrac{2}{{{x^2} - 4x + 4}}\)
a: \(=\dfrac{3b+4a}{6ab}\)
b: \(=\dfrac{x^2-2x+1-x^2-2x-1}{x^2-1}=\dfrac{-4x}{x^2-1}\)
c: \(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xy}{xyz}=\dfrac{z-x}{xz}\)
d: \(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: \(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)
Đúng 1
Bình luận (0)