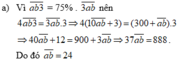a , Số đó là :72 vì 72:9=8

                              7-2=5

 b , Số đó là : 24 vì 24:3=8

                               2x4=8

a, Gọi số tự nhiên có hai chữ số là a b .

Ta có  a b ⋮ 9 nên a+b ⋮ 9 suy ra a+b = 9 

Thay a = 5+b vào a+b = 9, ta có:

5+b+b = 9 => 2b = 9 – 5 => 2b = 4 => b = 2

Ta có a+b = 9 => a = 9 – b => a = 9 – 2 => a = 7

Vậy số cần tìm là: 27 hoặc 72 (do đề bài không yêu cầu thứ tự các chữ số).

b, Gọi số tự nhiên có hai chữ số là  a b .

Ta có  a b ⋮ 3 nên  a+b ⋮ 3 suy ra a+b ∈ {3,6,9}

Ta lại có ab = 8 nên:

TH1: (a+b) = 3 và ab = 8 không có giá trị a, b thỏa điều kiện.

TH2: (a+b) = 6 và ab = 8 suy ra  a = 2 b = 4 hoặc  a = 4 b = 2

TH3: (a+b) = 9 và ab = 8 suy ra  a = 1 b = 8   hoặc  a = 8 b = 1

Vậy số cần tìm là: 24; 42; 18; 81.

Bài 1 nếu chia hết cho 3 thì 7a5b1 thì \(\frac{7a5b1}{3}=\frac{\left(7+5+1+a+b\right)}{3}=\frac{13+\left(a+b\right)}{3}\)

\(\Rightarrow a+b=2;5;8\)

\(a+b=2\left(loại\right)\)(hiệu k thể > hơn tổng)

\(a+b=5\left(loại\right)\)(vì để tìm \(\frac{b:\left(5-4\right)}{2}=0,5\)mà a và b là số tự nhiên =>a+b=8

\(a=\frac{8+4}{2}=6\)\(b=6-4=2\)

Vậy số cần tìm là 76521

76521

76521

Bài 1 nếu chia hết cho 3 thì 7a5b1 thì 

a+b=2(loại)a+b=2(loại)(hiệu k thể > hơn tổng)

a+b=5(loại)a+b=5(loại)(vì để tìm mà a và b là số tự nhiên =>a+b=8

Vậy số cần tìm là 76521

Vì 1110 là tổng của ba số tự nhiên nên => ta có a phải bằng 1000, b=100, c=10

Đáp số : a=1000

             b=100

             c=10

Nhớ ủng hộ nhé (^-^)

1.vì ƯCLN 2 số là 28 nên đặt a=28k, b=28p, k,p là số tự nhiênta có 28(k+p)=224=>k+q=8vậy các cặp (a, b) thỏa mãn là (28,196), (56, 168), (84,140), (112, 112)và các hoán vị của nó.

2.Dựa vào dữ kiện đề bài,ta có:

a=18k;b=18p.(k,p nguyên tố cùng nhau)

Tích:a.b=18k.18p

=324.k.p=1944

=>k.p=6.

=>k bằng 3;p=2.

Vậy a=54;p=36.

3.ĐK a > 12 ( số chia phải lớn hơn dư )

156 chia a dư 12 => 156 - 12 chia hết cho a => 144 chia hết cho a (1)

280 chia a dư 10 => 280 - 10 chia hết cho a => 270 chia hết cho a (2)

Từ (1) và (2) => 144 ; 270 chia hết cho a 

=> a thuộc UC (144;270)

UCLN ( 144 ; 270 ) =  18 

=> a thuộc ( 18 ; 9 ; 6 ; 3 ; 1 ) 

a > 12 => a= 18 

Bài 1:

Gọi hai số tự nhiên cần tìm là a,b

Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)

Tổng của hai số là 100 nên a+b=100(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)

Bài 2:

Gọi hai số cần tìm là a,b

Hiệu của hai số là 10 nên a-b=10(4)

Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)

Từ (3) và (4) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)

Bài 3:

Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)

Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)

Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:

\(\overline{ab}+\overline{ba}=77\)

=>\(10a+b+10b+a=77\)

=>11a+11b=77

=>a+b=7(6)

Từ (5) và (6) ta có hệ phương trình:

\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)

Vậy: Số tự nhiên cần tìm là 16

A là STN nhỏ nhất có 2 chữ số suy ra A = 10

B là STN lớn nhất có 3 chữ số suy ra B = 999

C là STN nhỏ nhất có 4 chữ số suy ra C = 1000

10=2.5

999= 3 mũ 2 . 111

1000= 10 mũ 3

BCNN( 10, 100,999)= 2.5.3 mũ 2.111. 10 mũ 3= 9990000