Cho đường tròn (O), đường kính AB. M là một điểm di động trên đường tròn. H là hình chiếu của M trên AB. Có bao nhiêu vị trí của M để diện tích tam giác OMH lớn nhất?

Những câu hỏi liên quan
cho đường tròn (O) đường kính AB=2r .Một điểm M di động trên (O) .Gọi H là hình chiếu của M trên AB .Số vị trí của điểm M để chu vi tam giác OMH lớn nhất
cho đg tròn (o) đg kính AB=2r .Một điểm M di động trên (O).Gọi H là hình chiếu của M trên AB.Số vị trí của điểm M để chu vi tam giác OMH lớn nhất ??? giúp mk vx nhé !!@@ ----cảm ơn nhiu
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.a. tứ giác ACOD là hình jb. tam giác BCD là tam giác jc. tính chu vi và diện tích tam giác BCD3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.a. CM: tứ giác BHCD là hình...
Đọc tiếp
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
giúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.a. tứ giác ACOD là hình jb. tam giác BCD là tam giác jc. tính chu vi và diện tích tam giác BCD3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.a. CM: tứ giác BHCD...
Đọc tiếp
giúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABC
giúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.a. tứ giác ACOD là hình jb. tam giác BCD là tam giác jc. tính chu vi và diện tích tam giác BCD3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.a. CM: tứ giác BHCD...
Đọc tiếp
giúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABC.
cho nửa đường tròn O đường kính AB=10cm 2 điểm C,D di động trên nửa đường tròn sao cho CD=8cm gọi M,N lần lượt là hình chiếu của A,B. Trên đường thẳng CD xác định vị trí của dây CD để tứ giác ABMN có diện tích lớn nhất.tính diện tích lớn nhất đó.
( gợi ý : sử dụng đường trung bình của hình thang )
Cho nửa đường tròn đường kính BC = 2R tâm O cố định. Điểm A di động trên nửa đường tròn. Gọi H là hình chiếu của điểm A trên BC. Gọi D và E lần lượt là hình chiếu của H trên AC và AB. Xác định vị trí điểm A sao cho tứ giác AEHD có diện tích lớn nhất? Tính diện tích lớn nhất đó theo R
Hình tự vẽ nha bạn :>
Xét ΔABCΔABC có AO = OB = OC
⇒ΔABC⇒ΔABC có trung tuyến AO ứng với một cạnh và = 1212 cạnh ấy
⇒ΔABC⇒ΔABC vuông ⇒BACˆ=90o⇒BAC^=90o
Dễ dàng c/m tứ giác ADHEADHE là hcn (Aˆ=Dˆ=EˆA^=D^=E^ =1v)
⇒EH=AD⇒EH=AD
Theo HTL, ta có :
{AB.BE=BH2AC.EH=AC.AD=AH2{AB.BE=BH2AC.EH=AC.AD=AH2
⇒AB.EB+AC.EH=BH2+AH2=AB2⇒AB.EB+AC.EH=BH2+AH2=AB2(đpcm)Hình tự vẽ nha bạn :>
Xét ΔABCΔABC có AO = OB = OC
⇒ΔABC⇒ΔABC có trung tuyến AO ứng với một cạnh và = 1212 cạnh ấy
⇒ΔABC⇒ΔABC vuông ⇒BACˆ=90o⇒BAC^=90o
Dễ dàng c/m tứ giác ADHEADHE là hcn (Aˆ=Dˆ=EˆA^=D^=E^ =1v)
⇒EH=AD⇒EH=AD
Theo HTL, ta có :
{AB.BE=BH2AC.EH=AC.AD=AH2{AB.BE=BH2AC.EH=AC.AD=AH2
⇒AB.EB+AC.EH=BH2+AH2=AB2⇒AB.EB+AC.EH=BH2+AH2=AB2(đpcm)
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính AB và một điểm M chuyển động trên nửa đường tròn đó. Hãy xác định vị trí của điểm M để sao cho diện tích tam giác MAB là lớn nhất.
Cho hình nón đỉnh N, đáy là hình tròn tâm O, góc ở đỉnh bằng
120
0
. Trên đường tròn đáy lấy một điểm A cố định và một điểm M di động. Gọi S là diện tích của tam giác NAM. Có bao nhiêu vị trí của điểm M để S đạt giá trị lớn nhất A. Vô số vị trí B. Hai vị trí C. Ba vị trí D. Một vị trí
Đọc tiếp
Cho hình nón đỉnh N, đáy là hình tròn tâm O, góc ở đỉnh bằng 120 0 . Trên đường tròn đáy lấy một điểm A cố định và một điểm M di động. Gọi S là diện tích của tam giác NAM. Có bao nhiêu vị trí của điểm M để S đạt giá trị lớn nhất
A. Vô số vị trí
B. Hai vị trí
C. Ba vị trí
D. Một vị trí
Chọn đáp án B
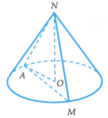
Gọi l l > 0 là độ dài đường sinh của hình nón. Vi góc ở đình bằng 120 0 nên A N O ⏜ = 60 0
Bán kính đường tròn đáy là
R = O A = N A . sin A N O ⏜ = l 3 2
Vì hình nón có góc ở đỉnh bằng 120 0 nên
![]()
Suy ra
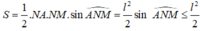
Dấu “=” xảy ra khi và chỉ khi
![]()
khi đó ∆ A N M vuông cân tại N ⇒ A M = l 2
Do A cố định nên M nằm trên đường tròn A ; l 2
Mặt khác M thuộc đường tròn đáy 0 ; l 3 2 nên M là giao điểm của đường tròn A ; l 2 và đường tròn 0 ; l 3 2
Vậy có hai vị trí của điểm M
Đúng 0
Bình luận (0)










