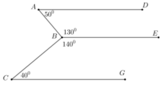
Cho hình vẽ sau. Hãy chứng tỏ AD // CG
Hãy vẽ hình tam giác ABC có ba góc nhọn rồi vẽ đường cao AD,BE,CG của hình tam giác đó . Em có nhận xét gì về các đường cao AD,BE,CG của hình tam giác này
Ba đường này cắt nhau tại một điểm gọi là trực tâm của tam giác
cho tam giác abc, d và g là điểm chính giữa của bc và ac, bg cắt ad ở e. Hãy chứng tỏ rằng ae gấp đôi ed.(vẽ hình luôn cho mình với)
Cho hình vẽ a) Chứng tỏ AD ||BC. b) Tính số đo C.
a) Ta có:
\(\widehat{A}=\widehat{B}=60^o\)
Mà 2 góc này ở vị trí đồng vị với nhau
=> AD // BC
b) Gọi 2 góc D là lượt là D1 và D2 (trong đó D2 = 106o)
Ta có:
\(\widehat{D_1}+\widehat{D_2}=180^o\) (kề bù)
\(\widehat{D_1}=180^o-\widehat{D_2}=180^o-106^o=74^o\)
Mà góc D1 và góc C đồng vị nhau
=> \(\widehat{D_1}=\widehat{C_1}=74^o\)
Cho hình vẽ biết:
A B ⊥ A C ; D A C ^ = 140 0 ; B ^ = 50 0 ; C ^ = 40 0
Chứng tỏ rằng :
a) AD//CF
b) AD//BE
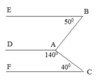
D A B ^ = 360 0 − 140 0 + 90 0 = 130 0
a) D A C ^ + A C F ^ = 140 0 + 40 0 = 180 0
Suy ra AD//CF( vì có cặp góc trong cùng phía bù nhau).
b) D A B ^ + A B E ^ = 130 0 + 50 0 = 180 0
Suy ra AD//BE( vì có cặp góc trong cùng phía bù nhau)
Cho hình vẽ dưới dây, hãy chứng tỏ a//b
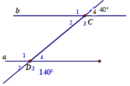
Tính góc D ^ 4 = 180 ° − 40 ° = 140 ° ( kề bù) mà D ^ 4 , C 4 ^ là 2 góc đồng vị => a // b
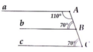
Cho hình vẽ bên. Hãy chứng tỏ a //b//c
Cho tam giác ABC,vẽ đường trung tuyến AD,BE,CF.Đường thẳng đi qua E và song song với AB ,đi qua F và song song với BE ,chúng cắt nhau tại G. Chứng minh:
a,AFEG là hình bình hành
b, D,E,G thẳng hàng
c, CG = AD
Xét tứ giác FGEB có :
FG//BE (gt)
GE//BF ( AB//GE , F ∈∈AB )
=> FGEB là hình bình hành
Vì FGEB là hình bình hành
=> FB = GE
Xét ∆ABC có :
F là trung điểm AB
E là trung điểm AC
=> FE là đường trung bình ∆ABC
=> FE //BC
Xét ∆ABC có :
E là trung điểm AC
D là trung điểm BC
=> ED là đường trung bình ∆ABC
=> ED//AB
Xét tứ giác FEDB có :
FE//BD ( FE//BC , D∈∈BC )
ED//FB ( ED//AB , F ∈∈AB )
=> FEDB là hình bình hành
=> FB = ED
Mà FB = GE (cmt)
=> FB = FA = GE = ED
Xét tứ giác AGEF có :
GE//FA (gt)
FA = GE (cmt)
=> AGEF là hình bình hành
Cho hình thôi ABCD. Trên AB lấy điểm E tùy ý, trên CD lấy điểm G sao cho CG=AE. Từ E và G vẽ các đường thẳng song song với BD, chúng lần lượt cắt AD và BC tại H và F. Chứng minh rằng:
a) EFGH là hình chữ nhật.
b) Hãy xác định vị trí của điểm E trên AB để EFGH là hình vuông.
Cho hình vẽ bên, biết BD = 9cm; CD = 16cm.
AB = 15cm.
a) Tính AD; AC.
b) Chứng tỏ góc BAC là góc vuông