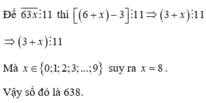Tìm x thích hợp để 61 x ¯ chia 11 dư 2

Những câu hỏi liên quan
Tìm x thích hợp để 36 x ¯ chia 7 dư 2
Bài 1. Thay a; b bằng những chữ số thích hợp để số 4̅̅𝑎̅̅2̅̅𝑏̅ chia hết cho 2; 5 và 9 Bài 2. Tìm a, b thích hợp để số 20̅̅̅̅𝑎̅2̅̅𝑏̅ chia hết cho cả 9 và 25. Bài 3. Thay x, y bởi những chữ số thích hợp để số 3̅̅𝑥̅̅57̅̅̅𝑦̅ chia 2 dư 1, chia 5 dư 3 và chia hết cho 9. Bài 4. Tìm số nhỏ nhất có 3 chữ số chia cho 2 dư 1; chia cho 5 dư 4 và chia cho 9 dư 7. Bài 5. Số bút chì cô giáo có ít hơn 35 chiếc và nhiều hơn 20 chiếc. Khi đem số bút chì đó chia cho 5 hoặc chia cho 3 thì vừa hết. Hỏi lúc đầu, cô g...
Đọc tiếp
Bài 1. Thay a; b bằng những chữ số thích hợp để số 4̅̅𝑎̅̅2̅̅𝑏̅ chia hết cho 2; 5 và 9 Bài 2. Tìm a, b thích hợp để số 20̅̅̅̅𝑎̅2̅̅𝑏̅ chia hết cho cả 9 và 25. Bài 3. Thay x, y bởi những chữ số thích hợp để số 3̅̅𝑥̅̅57̅̅̅𝑦̅ chia 2 dư 1, chia 5 dư 3 và chia hết cho 9. Bài 4. Tìm số nhỏ nhất có 3 chữ số chia cho 2 dư 1; chia cho 5 dư 4 và chia cho 9 dư 7. Bài 5. Số bút chì cô giáo có ít hơn 35 chiếc và nhiều hơn 20 chiếc. Khi đem số bút chì đó chia cho 5 hoặc chia cho 3 thì vừa hết. Hỏi lúc đầu, cô giáo có tất cả bao nhiêu chiếc bút chì? Bài 6. Trong một cuộc họp người ta xếp ghế thành 2 dãy, nếu mỗi ghế có 3 người ngồi thì số đại biểu ở 2 dãy bằng nhau. Nhưng nếu mỗi ghế có 5 người ngồi thì sẽ có 4 đại biểu ngồi riêng. Hãy tính số đại biểu tham gia cuộc họp, biết rằng số người dự họp là số lớn hơn 60 và nhỏ hơn 100
Bài 1:
Đặt \(X=\overline{4a2b}\)
X chia hết cho 2;5 nên X chia hết cho 10
=>X có chữ số tận cùng là 0
=>b=0
=>\(X=\overline{4a20}\)
X chia hết cho 9
=>\(\left(4+a+2+0\right)⋮9\)
=>\(\left(a+6\right)⋮9\)
=>a=3
vậy: X=4320
Bài 2:
Đặt \(A=\overline{20a2b}\)
A chia hết cho 25 mà A có tận cùng là \(\overline{2b}\)
nên b=5
=>\(A=\overline{20a25}\)
A chia hết cho 9
=>\(2+0+a+2+5⋮9\)
=>\(a+9⋮9\)
=>\(a⋮9\)
=>\(a\in\left\{0;9\right\}\)
Bài 3:
Đặt \(B=\overline{3x57y}\)
B chia 5 dư 3 nên B có tận cùng là 3 hoặc 8(1)
B chia 2 dư 1 nên B có tận cùng là số lẻ (2)
Từ (1),(2) suy ra B có tận cùng là 3
=>y=3
=>\(B=\overline{3x573}\)
B chia hết cho 9
=>\(3+x+5+7+3⋮9\)
=>\(x+18⋮9\)
=>\(x\in\left\{0;9\right\}\)
Đúng 1
Bình luận (0)
Bài 1. Thay a; b bằng những chữ số thích hợp để số 4̅̅𝑎̅̅2̅̅𝑏̅ chia hết cho 2; 5 và 9Bài 2. Tìm a, b thích hợp để số 20̅̅̅̅𝑎̅2̅̅𝑏̅ chia hết cho cả 9 và 25.Bài 3. Thay x, y bởi những chữ số thích hợp để số 3̅̅𝑥̅̅57̅̅̅𝑦̅ chia 2 dư 1, chia 5 dư 3 và chia hết cho 9Bài 5. Số bút chì cô giáo có ít hơn 35 chiếc và nhiều hơn 20 chiếc. Khi đem số bút chì đó chia cho 5 hoặc chia cho 3 thì vừa hết. Hỏi lúc đầu, cô giáo có tất cả bao nhiêu chiếc bút chì?
Đọc tiếp
Bài 1. Thay a; b bằng những chữ số thích hợp để số 4̅̅𝑎̅̅2̅̅𝑏̅ chia hết cho 2; 5 và 9
Bài 2. Tìm a, b thích hợp để số 20̅̅̅̅𝑎̅2̅̅𝑏̅ chia hết cho cả 9 và 25.
Bài 3. Thay x, y bởi những chữ số thích hợp để số 3̅̅𝑥̅̅57̅̅̅𝑦̅ chia 2 dư 1, chia 5 dư 3 và chia hết cho 9
Bài 5. Số bút chì cô giáo có ít hơn 35 chiếc và nhiều hơn 20 chiếc. Khi đem số bút chì đó chia cho 5 hoặc chia cho 3 thì vừa hết. Hỏi lúc đầu, cô giáo có tất cả bao nhiêu chiếc bút chì?
Bài 5:
Vì số bút chì khi đem chia 5 hoặc 3 thì vừa hết số bút chì sẽ vừa chia hết cho 5; vừa chia hết cho 3
=>Số bút chì sẽ chia hết cho 15
mà số bút chì có nhiều hơn 20 chiếc và ít hơn 35 chiếc
nên số bút chì là 30 chiếc


Đúng 1
Bình luận (0)
1)tìm số tự nhiên x lớn nhất , biết rằng 428 và 708 chia cho x đc số dư là 8
2)thấy các dấu * bằng c/số thích hợp để số 956** chia hết cho cả 6,7,27 và 11.
Toán lớp 6 nha bạn
1)Vậy 428 - 8 = 420 chia hết cho x và 708 - 8 = 700 chia hết cho x
420 = 22.3.5.7 700=22.52.7
x = UCLN(420 ; 700) = 22.5.7 = 140
2) 6=2.3 ; 7=7; 27 = 33 ; 11=11
BCNN(6;7;11;27) = 2.7.33.11= 4158
4158 x 23 = 95634
Vậy ta thay dấu ** được số 95634
Đúng 0
Bình luận (0)
1)tìm số tự nhiên x lớn nhất , biết rằng 428 và 708 chia cho x đc số dư là 8
2)thấy các dấu * bằng c/số thích hợp để số 956** chia hết cho cả 6,7,27 và 11.
Toán lớp 6 nha bạn
1)Vậy 428 - 8 = 420 chia hết cho x và 708 - 8 = 700 chia hết cho x
420 = 22.3.5.7 700=22.52.7
x = UCLN(420 ; 700) = 22.5.7 = 140
2) 6=2.3 ; 7=7; 27 = 33 ; 11=11
BCNN(6;7;11;27) = 2.7.33.11= 4158
4158 x 23 = 95634
Vậy ta thay dấu ** được số 95634
Đúng 0
Bình luận (0)
2)956** chia hết cho 6;7;11;27
=>956** là bội có 5 chữ số của BCNN(6;7;11;27)
Ta có:6=2.3
7=7
11=11
27=33
=>BCNN(6;7;11;27)=2.33.7.11=4158
=>956** là bội của 4158
=>956** là 95634
Đúng 0
Bình luận (0)
thay ab bằng chữ số thích hợp để số 2a83b chia hết cho 3 và chia 5 dư 1
tìm x,y biết 12x3ychia hết 45
tìm a sao cho 95a14 chia hết 11
chứng tỏ với mọi số tự nhiên N, tích (n+11)*(n+12) luôn chia hết cho 2
Tìm x thích hợp để 63 x ¯ chia hết cho 11.
Sơ đồ con đường |
Lời giải chi tiết |
Áp dụng dấu hiệu chia hết cho 7. |
Để 63 x ¯ ⋮ 11 thì 6 + x − 3 ⋮ 11 ⇒ 3 + x ⋮ 11 ⇒ 3 + x ⋮ 11 Mà x ∈ 0 ; 1 ; 2 ; 3 ; ... ; 9 suy ra x= 8. Vậy số đó là 638. |
Đúng 0
Bình luận (0)
Tìm x thích hợp để 63 x ¯ chia hết cho 11
Bài 1: Tìm số tự nhiên x lớn nhất sao cho: 13 ; 15 ; 61 chia x đều dư 1.
Bài 2: Tìm số tự nhiên x nhỏ nhất biết khi chia x cho các số 5; 7; 11 thì được các số dư lần lượt là 3; 4; 6.