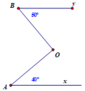
Cho hình vẽ dưới dây, biết rằng A x / / B y , chứng minh rằng B O ⊥ O A
Những câu hỏi liên quan
Cho điểm M ở ngoài (O,R). Vẽ tiếp tuyến MA với (O) tại tiếp điểm A. Vẽ dây AB ┴ OM tại H.a) Chứng minh rằng MB là tiếp tuyến của (O).b) Đoạn thẳng OM cắt (O) tại I. Chứng minh rằng I là tâm của đường tròn nội tiếp của tam giác MAB.c) Vẽ đường kính BC của (O). Chứng minh rằng: AC.MO 2R2.d) Cho OM 3R, chứng minh rằng: tích hai bán kính đường tròn ngoại tiếp và nội tiếp của tam giác MAB bằng R2 .
Đọc tiếp
Cho điểm M ở ngoài (O,R). Vẽ tiếp tuyến MA với (O) tại tiếp điểm A. Vẽ dây AB ┴ OM tại H.
a) Chứng minh rằng MB là tiếp tuyến của (O).
b) Đoạn thẳng OM cắt (O) tại I. Chứng minh rằng I là tâm của đường tròn nội tiếp của tam giác MAB.
c) Vẽ đường kính BC của (O). Chứng minh rằng: AC.MO = 2R2.
d) Cho OM = 3R, chứng minh rằng: tích hai bán kính đường tròn ngoại tiếp và nội tiếp của tam giác MAB bằng R2 .
a: Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MB là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho hai đường tròn (O;R) và (O';R') tiếp xúc ngoài tại A (R> R').Vẽ các đường kính AOB ,AO'C .Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC .
a/ Chứng minh rằng tứ giác BDCE là hình thoi
b/ Gọi I là giao điểm của EC và đường tòn (O').Chứng minh rằng 3 điểm D,A,I thẳng hàng
c/Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
Cho hai đườngtròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.
a) Chứng minh rằng tứ giác DBCE là hình thoi
b) Gọi I là giao điểm của EC và đường tròn (O'). Chứng minh rằng ba điểm D, A, I thẳng hàng
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
bài 2: cho hình vẽ biết:: Ax//Dy. chứng minh rằng A^+B^+O^=360 độ
Cho (O;R).từ điểm A nằm ngoài (O) sao cho OA2R vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm ) kẻ dây BC vuông góc OA
a) chứng minh : AC là tiếp tuyến của đường tròn(O)
b)Qua O vẽ đường vuông góc với OC cắt AB tại M. Chứng minh rằng: tam giác OMA tà tam giác cân
c) gọi N là giao điểm của OA với đường tròn (O) ,tia MN Cắt AC tại K .chứng minh rằng:MK là tiếp tuyến của đường tròn (O)
d) tính chu vi tam giác AMK theo R
Đọc tiếp
Cho (O;R).từ điểm A nằm ngoài (O) sao cho OA=2R vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm ) kẻ dây BC vuông góc OA a) chứng minh : AC là tiếp tuyến của đường tròn(O) b)Qua O vẽ đường vuông góc với OC cắt AB tại M. Chứng minh rằng: tam giác OMA tà tam giác cân c) gọi N là giao điểm của OA với đường tròn (O) ,tia MN Cắt AC tại K .chứng minh rằng:MK là tiếp tuyến của đường tròn (O) d) tính chu vi tam giác AMK theo R
a: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O;R)
b: \(\widehat{MOA}+\widehat{COA}=\widehat{MOC}=90^0\)
\(\widehat{MAO}+\widehat{BOA}=90^0\)(ΔBAO vuông tại B)
mà \(\widehat{COA}=\widehat{BOA}\)
nên \(\widehat{MOA}=\widehat{MAO}\)
=>ΔMAO cân tại M
Đúng 0
Bình luận (0)
Cho đường tròn (O) bán kính OA = R Vẽ dây BC vuông góc với OA tại trung điểm H của OA.
a) Tứ giác ABOC là hình gì? Vì sao?
b) Gọi K là điểm đối xứng với O qua A Chứng minh rằng K, B, O, C cùng thuộc một đường tròn
a: Xét tứ giác ABOC có
H là trung điểm của OA
H là trung điểm của BC
Do đó: ABOC là hình bình hành
mà OA=OB
nên ABOC là hình thoi
Đúng 1
Bình luận (0)
Cho ( O; 15cm) đường kính AB Vẽ dây CD vuông góc với OA tại H sao cho OH = 9cm. Gọi E là điểm đối xứng của A qua H a) Tính độ dài của dây BC b) Gọi I là giao điểm của DE và BC, Chứng minh rằng I thuộc ( O,) đường kính EB. c) Chứng minh rằng HI là tiếp tuyến của đường tròn tâm O
Cho đường tròn (O) và đường thẳng xy tiếp xúc với đường tròn tại A. Vẽ đường tròn (I) đường kính OA.
a) Chứng minh rằng hai đường tròn (O) và (I) tiếp xúc với nhau
b) Vẽ dây cung AC của (O) cắt I tại một điểm thứ hai là M. Chứng minh MA=MC
c) đường thẳng OM cắt xy tại B. Chứng minh rằng BC là tiếp tuyến của (O)
cho hai đường tròn (O:R)và (O':R') tiếp xúc ngoài tại A(r>R').Vẽ dây AB của (O)và dây AC của (O') sao cho AB vuông góc với AC.
a)chứng minh OB//O'C.
b)chứng mkinh rằng khi B thay đổi trên (O) thì BC đi qua 1 điểm cố định.