a) Xét tam giác ABC có: OE // BC (gt).

\(\Rightarrow\) \(\dfrac{AE}{AB}=\dfrac{AO}{AC}\left(Talet\right).\left(1\right)\)

Xét tam giác ACD có: OF // CD (gt).

\(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AO}{AC}\left(Talet\right).\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AE}{AB}.\)

Xét tam giác ABD có: \(\dfrac{AF}{AD}=\dfrac{AE}{AB}\left(cmt\right).\)

\(\Rightarrow\) EF // BD (định lý Talet đảo).

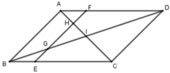
Có ABCD là hình bình hành nên: AD // BC, AB // DC

Xét ΔBGE và ΔDGF có:

B G E ^ = D G F ^ (đối đỉnh)

E B G ^ = F D G ^ (so le trong)

=> ΔBGE ~ ΔDGF (g-g) nên C đúng

Xét ΔAHF và ΔCHE có:

A H F ^ = C H E ^ (đối đỉnh)

H A F ^ = H C E ^ (so le trong)

=> ΔAHF ~ ΔCHE (g-g) nên D đúng

Lại có GH // AB ⇒ I H G ^ = I A B ^ (đồng vị)

Xét ΔGHI và ΔBAI có

Chung I

I H G ^ = I A B ^ (cmt)

=> ΔGHI ~ ΔBAI (g-g)

Suy ra B đúng

Chỉ có A sai.

Đáp án A