Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và C'D' bằng
A. a
B. a 2
C. a 3 2
D. a 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
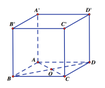
A. 2 a
B. a
C. 3 a
D. 3 2 a
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
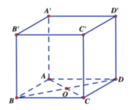
A. a 2
B. a.
C. a 3
D. a 3 2
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng

A. 2 a
B. a
C. 3 a
D. a 3 2
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng
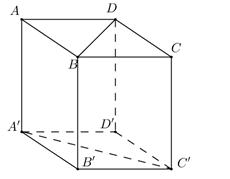
A. 2 a.
B. a.
C. 3 a.
D. 2 a 2
hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng AC và A′D bằng
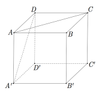
A. 2 2 a
B. 3 3 a
C. 3 6 a
D. 2 3 a
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CC′ bằng
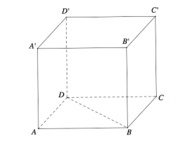
A. a/2.
B. a 2 4
C. a 2 2
D. a/4.
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B′C′ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B′D′ bằng
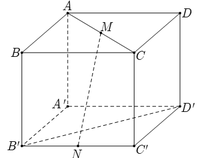
A. 5 a 5
B. a 3
C. 5 a
D. 3 a
Cho hình lập phương ABCD.A' B' C' D' có cạnh bằng 1. Khoảng cách giữa hai đường thẳng CD' và AB là
A. 1
B. 3
C. 2
D. 3 3
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D tới đường chéo AC' bằng nhau. Tính khoảng cách đó.
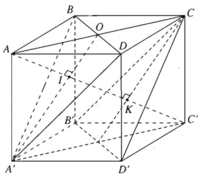
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:
C′B = C′D = C′A′ = a√2
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD
Ta lại có 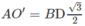
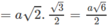
Vậy 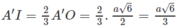
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.