Cho hình thang ABCD vuông A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 πa 3 3
B. V = 5 πa 3 3
C. V = 7 πa 3 3
D. V = πa 3
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;1), C(6;1;0) và đỉnh D(a,b,c). Biết rằng hình thang có diện tích là 6 2 , tính a+b+c
A. a+b+c=6
B. a+b+c=8
C. a+b+c=12
D. a+b+c=7
1, Cho hình thang ABCD ( AB // CD ) có góc B - góc C = 24° , góc A = 1,5 góc D . Tính các góc của hình thang .
2. Cho hình thang vuông ABCD ( góc A = góc D = 90°) đường chéo BD vuông góc với cạnh bên BC và BD = BC :
a, Tính các góc của hình thang .
b, Biết AB = 3 cm , Tính độ dài các cạnh BC,CD .
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng? A. a+b+c6 B. a+b+c5 C. a+b+c8 D. a+b+c7
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7
Chọn A
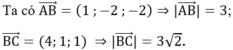
Theo giả thiết ABCD vuông tại A và B và có diện tích bằng 6√2 nên:
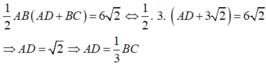
Do ABCD là hình thang vuông tại A và B nên 
. Giả sử khi đó ta có:
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có A ^ = D ^ = 90 0 , AB = AD = 2 cm, DC = 4 cm và BH vuông góc với CD tại H.
a) Chứng minh ∆ABD = ∆HDB.
b) Chứng minh tam giác BHC vuông cân tại H.
c) Tính diện tích hình thang ABCD
a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
Cho khối lăng trụ ABCD A B C D . ′′′′ có đáy ABCD là hình thang cân, AD BC // , BC a = ,
AD a AB a = = 3 , 2; góc giữa hai mặt phẳng ( ADD A′ ′) và ( ABCD) bằng 60 . ° Nếu A B′ vuông góc
với mặt phẳng ( ABCD) thì khối lăng trụ ABCD A B C D . ′′′′ có thể tích là
sai rồi bạn đạt
toán lớp 1 con k lm đc
Xem thêm câu trả lời
Cho hình thang vuông ABCD (góc A= góc D= 90 độ), đường chéo BD vuông góc với cạnh bên BC và bằng BC.
a) Tính các góc B và C của hình thang ABCD
b) CM: AB=AD
c)CM: CD=2AD
ét tam giác DBC có :
góc B = 90 độ ( BD vuông góc BC)
BD=BC
=> tam giác DBC là tam giác vuông cân => góc C =góc BDC= 45 độ
xét hình thang ABCD có :
góc ABC = 360 độ - ( 90 dộ+90 độ+45 độ) = 135 độ
b) ta có :
góc ABD = góc ABC - góc DBC = .135 độ - 90 độ = 45 độ
BD = cos ABD . AB = cos 45 độ . 3 = ......cm
mà BD=BC=> BC =.....cm
xét tam giác vuông cân DBC có
CD^2= BC^2 + BD^2 (định lí pi-ta-go)
<=>.................
<=>.................
=> CD =........cm
Đúng 0
Bình luận (1)
cho tứ giác ABCD có các tia phân giác góc A và góc D vuông góc với nhau. Chứng Minh:
a) ABCD là hình thang
b) 2 tia phân giac góc D và góc C vuông góc với nhau
cho tứ giác ABCD có các tia phân giác góc A và góc D vuông góc với nhau. Chứng Minh:
a) ABCD là hình thang
b) 2 tia phân giac góc D và góc C vuông góc với nhau
Cho hình thang vuông ABCD có góc A =góc B = 90° ;Ab = BC =1\2AD .
A,tính góc D và góc C
B,Chứng minh AD vuông góc với CD
C,biết AB =5cm,tính chu vi hình thang ABCD