Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
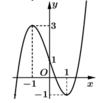
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Cho hàm số y=f(x) Hàm số y=f'(x) có đồ thị như hình bên
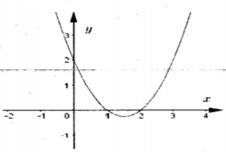
Hàm số y=f(1-3x) đồng biến trên khoảng
A. (1;2)
B . 2 ; + ∞
C . 0 ; 1 3
D . - 1 3 ; 0
Cho hàm số f (x) có đồ thị của hàm số f'(x) như hình vẽ bên.
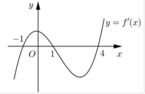
Biết f(-1)=f(4)=0. Hàm số y = ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
A. (-1;0).
B. (1;4).
C. ( - ∞ ; 1 ) .
D. ( 4 ; + ∞ ) .
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
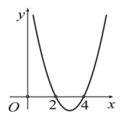
A. ( 3 ; + ∞ )
B. ( - 3 ; - 1 )
C. ( 1 ; 3 )
D. (0;1)

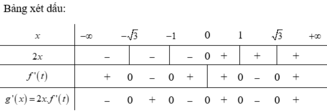
Vậy hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng ( 1 ; 3 )
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
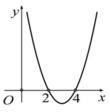
Cho hàm số y=f(x) có đồ thị y=f'(x) như hình bên
Hàm số y = f ( 1 - x 2 ) có bao nhiêu điểm cực trị
A. 1
B. 2
C. 3
D. 4
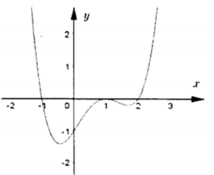
Cho hàm số y=f(x) có đồ thị y=f’(x) như hình vẽ bên. Biết f(a)>0, hỏi đồ thị hàm số y=f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
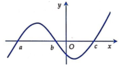
Cho hàm số y = f(x) có đồ thị y = f''(x) như hình vẽ bên. Biết f (a) > 0, hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.
Cho hàm số y=f(x). Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
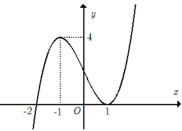
A. Hàm f(x) nghịch biến trên khoảng ( - ∞ ; - 2 )
B. Hàm f(x) đồng biến trên khoảng ( 1 ; + ∞ )
C. Trên (-1;1) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.
Cho hàm số y = f(x). Biết rằng hàm số f(x) có đạo hàm là f '(x) và hàm số y = f '(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
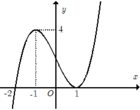
A. Hàm f (x) nghịch biến trên khoảng - ∞ ; - 2
B. Hàm f (x) đồng biến trên khoảng 1 ; + ∞
C. Trên - 1 ; 1 thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2