Tìm ƯCLN của 15, 45 và 225
A. 18
B. 3
C. 15
D. 5
Những câu hỏi liên quan
Tìm ƯCLN của 15, 45 và 225
A. 18
B. 3
C. 15
D. 5
Đáp án là C
Ta có: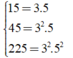
Vậy ƯCLN(15; 45; 225) = 15
Đúng 0
Bình luận (0)
Tìm ƯCLN (15,45): A.3 B.15 C.5 D.18
Xem thêm câu trả lời
ƯCLN( a;15)= 15 và BCNN(a;15)=45
Tìm a
b)
ƯCLN( a;42)= 6 và BCNN(a;42)=420
Tìm a
c) ƯCLN( a;378)= 18 và BCNN(a;378)=3780
Tìm a
3/5 của 135 là
A.27 B.81 C.225 D.45
Hiệu của hai số là 45, tỉ số của hai số đó là 1/4 . Hai số đó là:
A.30 VÀ 20 B.15 và 35 C.10 và 40 D.15 và 60
Câu 1: 3/5 x 135 = 81 => B
Câu 2:
Hiệu số phần bằng nhau là: 4 -1 = 3 phần
Số lớn là: 45 : 3 x 4 = 60
Số bé là: 90 - 45 = 15
=> D
Đúng 1
Bình luận (0)
\(\dfrac{3}{5}\) của 135 là: 135 \(\times\) \(\dfrac{3}{5}\) = 81
Chọn B. 81
Số bé bằng: 1:( 4-1) = \(\dfrac{1}{3}\) hiệu hai số
Số bé là: 45 \(\times\) \(\dfrac{1}{3}\) = 15
Số lớn là: 15 + 45 = 60
Chọn B. 15 và 30
Chọn D 15 và 60
Đúng 1
Bình luận (0)
Tìm ƯCLN rồi tìm BCNN của :
a.15 và 45 b.7,9và 12. c.12,14 và 18 d,11,33 và 99
a, 15 = 3 . 5
45 = 32 . 5
=> UCLN = 3 . 5 = 15
BCNN = 32 . 5 = 45
b, 7 = 1 . 7
9 = 32
12 = 22 . 3
=> UCLN = 1
BCNN = 32 . 22 . 7 = 252
c, 12 = 22 . 3
14 = 2. 7
18 = 2 . 32
UCLN = 2
BCNN = 22 . 32 . 7 = 252
d , 11 = 11 . 1
33 = 3 . 11
99 = 32 . 11
=> UCLN = 11
BCNN = 32 . 11 = 99
Đúng 0
Bình luận (0)
1. ƯCLN của hai số là 45. Số lớn là 270, tìm số bé.
2. Tìm hai số biết tổng của chúng là 162 và ƯCLN của chúng là 18.
3. Tìm hai số tự nhiên a và b, biết rằng BCNN(a,b) = 300; ƯCLN (a,b) = 15.
bài 1:
Gọi 2 số đó là a và 270 với a < 270
Ta có ƯCLN(a ; 270) = 45
=> a = 45m ; 270 = 45 . 6 (m ∈ N)
Mà ƯCLN(a ; 270) = 45 => ƯCLN(m ; 6) = 1
Do a < 270 nên m < 6.
Vậy m ∈ {1 ; 5}
Khi đó a ∈ {45 ; 225}
Vậy số bé là 45 hoặc 225
Bài 2:
Tìm 2 số có tổng là 162 và UCLN là 18.
x+y=162
x=18m; y=18n => m+n=9 và m, n nguyên tố cùng nhau => xảy ra 3 trường hợp
1. m=4; n=5 hoặc ngược lại
=> x=18*4=72 và y=18*5=90 hoặc ngược lại
2. m=1 và n=8 hoặc ngược lại
=> x=18 và y=144 hoặc ngược lại
3. m=2 và n=7 hoặc ngược lại
=> x=36 và y=126 hoặc ngược lại
Bài 3:
Vì BCNN(A,B)=300;ƯCLN(A,B)=15=> AB= 4500
ta có: ƯCLN(A,B)= 15=> A=15k;b=15q với ƯCLN(k;q)=1
=> 15k x 15q = 4500
=> 225kq=4500
=> kq= 20
Mà ƯCLN(k;q)=1 => ta có bảng:
| k | 1 | 4 | 5 | 20 |
|---|---|---|---|---|
| A | 15 | 60 | 75 | 300 |
| q | 20 | 5 | 4 | 1 |
| B | 300 | 75 | 60 | 15 |
Mà theo đề bài: A+15=B=> A=60; B=75
Đúng 0
Bình luận (0)
tìm 2 số a,b a>b biết a.b=300 và ucln[a,b]=5
Đúng 0
Bình luận (0)
bài 1:
Gọi 2 số đó là a và 270 với a < 270
Ta có ƯCLN(a ; 270) = 45
=> a = 45m ; 270 = 45 . 6 (m ∈ N)
Mà ƯCLN(a ; 270) = 45 => ƯCLN(m ; 6) = 1
Do a < 270 nên m < 6.
Vậy m ∈ {1 ; 5}
Khi đó a ∈ {45 ; 225}
Vậy số bé là 45 hoặc 225
Bài 2:
Tìm 2 số có tổng là 162 và UCLN là 18.
x+y=162x=18m; y=18n => m+n=9 và m, n nguyên tố cùng nhau => xảy ra 3 trường hợp1. m=4; n=5 hoặc ngược lại=> x=18*4=72 và y=18*5=90 hoặc ngược lại2. m=1 và n=8 hoặc ngược lại=> x=18 và y=144 hoặc ngược lại3. m=2 và n=7 hoặc ngược lại=> x=36 và y=126 hoặc ngược lại
Bài 3:
Vì BCNN(A,B)=300;ƯCLN(A,B)=15=> AB= 4500
ta có: ƯCLN(A,B)= 15=> A=15k;b=15q với ƯCLN(k;q)=1
=> 15k x 15q = 4500
=> 225kq=4500
=> kq= 20
Mà ƯCLN(k;q)=1 => ta có bảng:
| k | 1 | 4 | 5 | 20 |
|---|---|---|---|---|
| A | 15 | 60 | 75 | 300 |
| q | 20 | 5 | 4 | 1 |
| B | 300 | 75 | 60 | 15 |
Mà theo đề bài: A+15=B=> A=60; B=75
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1 tìm ƯCLN của các số
a] ƯCLN [ 18 ; 30 ] b] ƯCLN [ 24 ; 48 ]
c] ƯCLN [ 18 ; 30 ;15 ] d] ƯCLN [ 24 ; 48 ; 36 ]
2 sử dụng thuật toán Ơclit để tìm
a] ƯCLN [ 174 ; 18 ] B] ƯCLN [ 124 ; 16 ]
1)
a) 18 = 2.3²
30 = 2.3.5
ƯCLN(18; 30) = 2.3 = 6
b) 24 = 2³.3
48 = 2⁴.3
ƯCLN(24; 48) = 2³.3 = 24
c) 18 = 2.3²
30 = 2.3.5
15 = 3.5
ƯCLN(18; 30; 15) = 3
d) 24 = 2³.3
48 = 2⁴.3
36 = 2².3²
ƯCLN(24; 48; 36) = 2².3 = 12
Đúng 2
Bình luận (0)
2) a) 174 = 18 . 9 + 12
18 = 12 . 1 + 6
12 = 6 . 2
Vậy ƯCLN(174; 18) = 6
b) 124 = 16 . 7 + 12
16 = 12 . 1 + 4
12 = 4 . 3
⇒ ƯCLN(124; 16) = 4
⇒ BCNN(124; 16) = 124 . 16 : 4 = 496
Đúng 2
Bình luận (0)
: a) Tìm các tập hợp B(6), B(9), B(12) , Ư(30), Ư(45), Ư(60)
b) Tìm ƯCLN(36, 48), ƯCLN(24; 28; 36);
c) Tìm BCNN(6,8), BCNN(8, 9, 72);
d) Tìm BCNN của 15 và 54. Từ đó, hãy tìm ra các bội chung nhỏ hơn 1000 của 15 và 54
Tìm ƯCLN của
a) 18; 30
b) 24; 48
c) 18; 30; 15
d) 24; 48; 36
a) 18 = 2 . 3 2 ; 30 = 2 . 3 . 5 . Từ đó ƯCLN (18; 30) = 2.3 = 6.
b) 24 = 2 3 . 3 ; 48 = 2 4 . 3 . Từ đó Ư C L N ( 24 ; 48 ) = 2 3 . 3 = 24 .
c) 18 = 2 . 3 2 ; 30 = 2 . 3 . 5 ; 15 = 3 . 5 . Từ đó ƯCLN (18; 30; 15) = 3.
d) 24 = 2 3 . 3 ; 48 = 2 4 . 3 ; 36 = 2 2 . 3 2 .
Từ đó Ư C L N ( 24 ; 48 ; 36 ) = 2 2 . 3 = 12 .
Đúng 2
Bình luận (1)