Giá trị nào sau đây của x để giá trị phân thức x - 2 x + 3 là nguyên
A. 1
B. 2
C. 3
D. 4
Giá trị nào sau đây của x để giá trị phân thức x x + 1 là nguyên
A. 1
B. -1
C. 2
D. -2
Đáp án: D
Điều kiện xác định của phân thức: x ≠ - 1
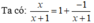
Để  nguyên ⇒ x + 1 là ước của -1 hay x + 1 ∈ {-1;1}
nguyên ⇒ x + 1 là ước của -1 hay x + 1 ∈ {-1;1}
Với x + 1 = -1 ⇔ x = - 2 (thỏa mãn ĐKXĐ)
Với x + 1 = 1 ⇔ x = 0 (thỏa mãn ĐKXĐ)
Vậy đáp án D là đáp án đúng
Giá trị nào sau đây của x để giá trị phân thức 12 x + 12 3 x + 1 là nguyên
A. -1
B. 17
C. 0
D. 4
Đáp án: C
ĐKXĐ: x ≠ - 1 3
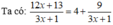
Để  nguyên ⇒ 3x + 1 là ước của 9 hay 3x + 1 ∈ {-9;-3;-1;1;3;9}
nguyên ⇒ 3x + 1 là ước của 9 hay 3x + 1 ∈ {-9;-3;-1;1;3;9}

Giá trị nào sau đây của x để giá trị phân thức 4 x - 5 2 x + 1 là nguyên
A. 3
B. 5
C. 7
D. 9
Đáp án: A
ĐKXĐ: x ≠ - 1 2
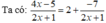
Để  nguyên ⇒ 2x + 1 là ước của -7 hay 2x + 1 ∈ {-7;-1;1;7}
nguyên ⇒ 2x + 1 là ước của -7 hay 2x + 1 ∈ {-7;-1;1;7}
Với 2x + 1 = -7 ⇔ 2x = - 8 ⇔ x = -4 (thỏa mãn ĐKXĐ)
Với 2x + 1 = -1 ⇔ 2x = - 2 ⇔ x = -1 (thỏa mãn ĐKXĐ)
Với 2x + 1 = 1 ⇔ 2x = 0 ⇔ x = 0 (thỏa mãn ĐKXĐ)
Với 2x + 1 = 7 ⇔ 2x = 6⇔ x = 3 (thỏa mãn ĐKXĐ)
Vậy đáp án A là đáp án đúng
Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
a) \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
Bài 2: (3 điểm) Cho phân thức \(\dfrac{3x+3}{x^2-1}\)
a/ Tìm điều kiện của x để giá trị của phân thức được xác định.
b/ Tìm giá trị của x để phân thức có giá trị bằng –2 .
c/ Tìm giá trị của x để phân thức có giá trị là số nguyên.
phân thức được xác định ⇔ x2 - 1 ≠ 0 ⇔ x ≠ \(\left\{-1;1\right\}\)
\(\dfrac{3x+3}{x^2-1}=-2\)
=> 3x + 3 = -2x2 + 2
=> 2x2 + 3x + 1 = 0
=> (2x+1)(x+1) = 0
=> x = -1/2 (thỏa mãn) hoặc x = -1 (loại)
Vậy, để phân thức có giá trị bằng –2 thì x = -1/2.
\(\dfrac{3x+3}{x^2-1}\)=\(\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\) (x khác -1 và x khác 1)
= \(\dfrac{3}{x-1}\)
=> Phân thức ban đầu có giá trị nguyên ⇔ 3 chia hết cho x-1
=> x-1 ∈\(\left\{-3;-1;1;3\right\}\)
=> x ∈\(\left\{-2;0;2;4\right\}\)
Vậy, để phân thức có giá trị là số nguyên.thì x ∈\(\left\{-2;0;2;4\right\}\).
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{3x+3}{x^2-1}\)
\(=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{3}{x-1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{3}{x-1}=-2\)
\(\Leftrightarrow x-1=-\dfrac{3}{2}\)
hay \(x=-\dfrac{1}{2}\)(thỏa ĐK)
Bài 2: (3 điểm) Cho phân thức \(\dfrac{3x+3}{x^2-1}\)
a/ Tìm điều kiện của x để giá trị của phân thức được xác định.
b/ Tìm giá trị của x để phân thức có giá trị bằng –2 .
c/ Tìm giá trị của x để phân thức có giá trị là số nguyên.
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{3x+3}{x^2-1}\)
\(=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{3}{x-1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{3}{x-1}=-2\)
\(\Leftrightarrow x-1=\dfrac{-3}{2}\)
hay \(x=-\dfrac{1}{2}\)
Vậy: Để phân thức có giá trị bằng -2 thì \(x=-\dfrac{1}{2}\)
c) Để phân thức có giá trị là số nguyên thì \(3⋮x-1\)
\(\Leftrightarrow x-1\inƯ\left(3\right)\)
\(\Leftrightarrow x-1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow x\in\left\{2;0;4;-2\right\}\)
Kết hợp ĐKXĐ, ta được:
\(x\in\left\{2;0;4;-2\right\}\)
Vậy: Để phân thức có giá trị là số nguyên thì \(x\in\left\{2;0;4;-2\right\}\)
Giá trị nào sau đây của x để giá trị phân thức 4 x - 7 x là nguyên
A. 4
B. -4
C. 7
D. 14
Đáp án: C
ĐKXĐ: x ≠ 0
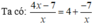
Để  nguyên ⇒ x là ước của -7 hay x ∈ {-7;-1;1;7}
nguyên ⇒ x là ước của -7 hay x ∈ {-7;-1;1;7}
Với các giá trị x = {-7;-1;1;7} thì phân thức 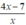 nhận giá trị nguyên
nhận giá trị nguyên
Vậy đáp án C là đáp án đúng
Cho phân thức :\(\dfrac{3x+3}{x^2-1}\)
a) Tìm điều kiện của x để giá trị của phân thức được xác định . Tìm giá trị của x để phân thức có giá trị bằng -2
b) Tìm giá trị của x để phân thức có giá trị là số nguyên
\(a,ĐK:x^2-1=\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne\pm1\\ \dfrac{3x+3}{x^2-1}=\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x-1}=2\\ \Leftrightarrow x-1=\dfrac{3}{2}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\\ b,\dfrac{3}{x-1}\in Z\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\left(tm\right)\)
Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
\(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
ĐKXĐ: \(x\ne1\)
Ta có: \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
\(=\dfrac{x^4-2x^3+x^2-4x^2+8x-4+3}{x^2-2x+1}\)
\(=\dfrac{x^2\left(x^2-2x+1\right)-4\left(x^2-2x+1\right)+3}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)^2\cdot\left(x^2-4\right)+3}{\left(x-1\right)^2}\)
\(=x^2-4+\dfrac{3}{\left(x-1\right)^2}\)
Để B nguyên thì \(3⋮\left(x-1\right)^2\)
\(\Leftrightarrow\left(x-1\right)^2\inƯ\left(3\right)\)
\(\Leftrightarrow\left(x-1\right)^2\in\left\{1;3;-1;-3\right\}\)
mà \(\left(x-1\right)^2>0\forall x\) thỏa mãn ĐKXĐ
nên \(\left(x-1\right)^2\in\left\{1;3\right\}\)
\(\Leftrightarrow x-1\in\left\{1;9\right\}\)
hay \(x\in\left\{2;10\right\}\) (nhận)
Vậy: \(x\in\left\{2;10\right\}\)