BÀI 1 : Ta có tam giác ABC có góc B=góc C=>tam giác ABC cân tại A =>AB=AC

BÀI 2:TA có:tam giác ABC có AB=AC=>Tam giác ABC cân tại A mak koa góc A = 6O độ =>tam giác ABC đều=>AB=AC=BC

                          TICK NHA, MK GIẢI CHI TIẾT LẮM RÙI ĐÓ

#\(N\)

`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:

`AM` chung

`AB = AC (g``t)`

\(\widehat{AMB}=\widehat{AMC}=90^0\)

`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`

`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`

`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`

`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`

`=> AM` là tia phân giác của \(\widehat{BAC}\)

`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:

`AM` chung

\(\widehat{HAM}=\widehat{KAM}(CMT)\)

`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`

`=> AH = AK (2` cạnh tương ứng `)`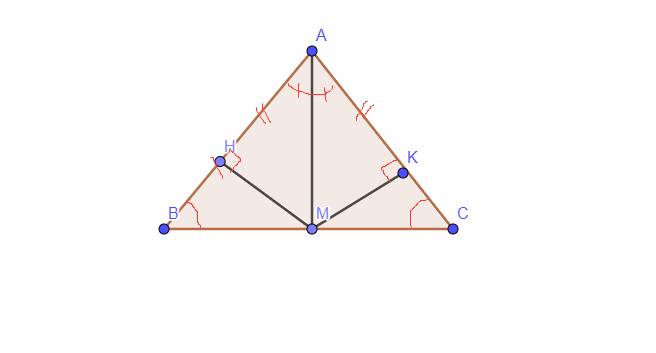

a, Xét ΔABC có AB=AC

=> ΔABC là tam giác cân

=> Góc B = góc C (t/c)

b, Xét ΔABC có: góc A + góc B + góc C = 180 độ ( tổng 3 góc trong 1 tam giác)

=> 180 - góc A = góc B + góc C (1)

mà ΔABC là tam giác cân => góc B = góc C (2)

Xét ΔAED có AE=AD => ΔAED là tam giác cân

=> góc E = góc D (3)

Chứng minh tương tự ta có 180 độ - góc A = góc AED + góc ADE (4)

Từ (1),(2),(3),(4) => góc ADE = góc B

( bạn tự vẽ hình)

a, xét tam giác ABE và tam giác ACE có:

AE chung

AB=AC (gt)

góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)

=> tam giác ABE=tam giác ACE

b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)

=> góc BEA=góc CEA ( 2 góc tương ứng)

mà 2 góc này kề bù

=> góc BEA=góc CEA= 180 độ : 2= 90 độ 

=> AE vuông góc với BC (2)

từ (1) và (2) ta có AE là đường trung trực của BC.

a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ 
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.

Kẻ trung tuyến AM, AM = 1/2 BC = MB = MC

a) Nêu góc B = 30 độ thì góc C bằng 60 độ

Tam giác MAC cân tại M có góc C bằng 60 độ nên nó là tam giác đều => AC = MC = 1/2 BC

b) Nếu AC = 1/2 BC => Tam giác MAC đều vì AC = 1/2 BC = MC = MA

=> Góc C bằng 60 độ

Trong tam giác ABC có góc A = 90 độ, góc C = 60 độ => góc B = 30 độ

sao lại làm thế này

i love việt nam

bạn lừa mình à :v

rảnh quá bạn ơi người ta nhờ giải bài hộ lên đây tang luôn câu 'i love việt nam ' 

 tam giác ABC có góc B= góc C suy ra tam giác này là tam giác cân

mà tam giác cân thì hai cạnh bên bằng nhau nên AB = AC

Mik chưa hc tam giác cân b

Lời giải:

$S_{ABC}=\frac{BD.AC}{2}=\frac{CE.AB}{2}$

$\Rightarrow \frac{BD}{CE}=\frac{AB}{AC}$

$CE-BD=\frac{BD.AC}{AB}-BD=\frac{BD}{AB}(AC-AB)$

Rõ ràng $BD< AB$ do cạnh huyền thì luôn lớn hơn cạnh góc vuông.

Và $AC-AB>0$ do $\widehat{B}>\widehat{C}$

$\Rightarrow CE-BD< AC-AB$ (đpcm)

Hình vẽ: