Mặt tiếp xúc với phoi là:
A. Mặt trước
B. Mặt sau
C. Mặt đáy
D. Cả 3 đáp án trên
Mặt tiếp xúc với phoi là:
A. Mặt trước
B. Mặt sau
C. Mặt đáy
D. Cả 3 đáp án trên
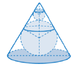
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là 2 β = 60 ° bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nó. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.
A. 25 3 π c m 3
B. 112 3 π c m 3
C. 40 3 π c m 3
D. 10 3 π c m 3
Đáp án B
Phương pháp:
Tính bán kính hai khối cầu dựa vào các mối quan hệ đường tròn nội tiếp tam giác.
Tính thể tích hai khối cầu đã cho theo công thức V = 4 3 π . R 3 và suy ra kết luận.
Cách giải: Cắt món đồ chơi đó bằng mặt phẳng đứng đi qua trục hình nón.
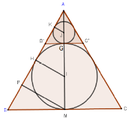
Gọi P, H, K lần lượt là hình chiếu vuông góc của M, I, J trên AB.
Vì B A C = 2 β = 60 ° , A M = 9 c m .
⇒ B M = M C = 3 3 A B = A C = 6 3 = B C ⇒ Δ A B C đều.
Vì IM là bán kính mặt cầu nội tiếp tam giác đều ABC nên I H = I M = A M 3 = 3
Gọi là tiếp tuyến chung của hai đường tròn. Vì Δ A B C đều nên dẫn đến Δ A B ' C ' đều.
Suy ra bán kính đường tròn nội tiếp:
J K = J G = A G 3 = A M 9 = 1
Vậy tổng thể tích là:
V 1 + V 2 = 4 3 π . I H 3 + 4 3 π . J K 3 = 112 π 3
Chú ý khi giải:
Cần chú ý vận dụng các mối quan hệ đường tròn nội, ngoại tiếp tam giác đều trong việc tính bán kính các khối cầu.
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là 2 β = 60 o bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nó. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.
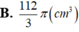
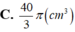
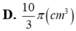
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
![]()
![]()
![]()
![]()
Một hình trụ có tâm các đáy là A,B. Biết rằng mặt cầu đường kính AB tiếp xúc với các mặt, đáy của hình trụ tại A,B và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 16 π . Tính diện tích xung quanh của mặt trụ đã cho.
A . 16 π 3
B . 16 π
C . 8 π
D . 8 π 3
Đáp án B.
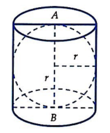
Gọi r là bán kính của mặt cầu nối tiếp
=> Diện tích xung quanh của mặt cầu là ![]()
![]()
=> Chiều cao của hình trụ là 4
=> Diện tích của hình trụ là ![]()
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo tra một mặt nón tròn xoay có góc ở đỉnh là
2
β
=
60
°
bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.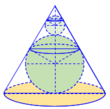
![]()
![]()
![]()
![]()
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo tra một mặt nón tròn xoay có góc ở đỉnh là
2
β
=
60
°
bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.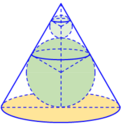
![]()
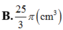
![]()
![]()
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO'
a) Chứng minh rằng mặt cầu đường kính OO' tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ
b) Cắt hình trụ bởi một mặt phẳng song song với trục OO' và cách trục một khoảng bằng \(\dfrac{r}{2}\). Tính diện tích thiết diện thu được
c) Thiết diện nói trên cắt mặt cầu đường kính OO' theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Chứng minh rằng mặt cầu đường kính OO’ tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ.
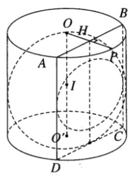
Vì các mặt đáy của hình trụ vuông góc với trục OO’ tại O và O’ nên chúng tiếp xúc với mặt cầu đường kính OO’.
Gọi I là trung điểm của đoạn OO’. Ta có I là tâm của mặt cầu. Kẻ IM vuông góc với một đường sinh nào đó (M nằm trên đường sinh) ta đều có IM = r là bán kính của mặt trụ đồng thời điểm M cũng thuộc mặt cầu. Vậy mặt cầu tiếp xúc với tất cả các đường sinh của mặt trụ.