Lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều, M là trung điểm BC, biết AA’ = AM = 2cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính thể tích lăng trụ.
Lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều, M là trung điểm BC, biết AA’ = AM = 2cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính thể tích lăng trụ.
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy là các tam giác vuông tại B và B', AA' = 5 cm, AB = 2 cm, AC = 6 cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính diện tích toàn phần lăng trụ.
c) Tính thể tích lăng trụ
a) Diện tích xung quanh của hình lăng trụ là: (2.6):2.5=30(m2) b) Diện tích toàn phần của hình lăng trụ là: 30+2.(2.6):2=42(m2) c) Thể tích của hình lăng trụ là: 5.(2.6):2=30(m3) Đáp số: a) 30m2; b) 42m2; 30m3
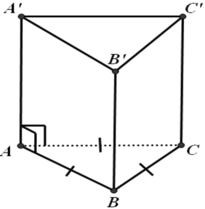
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều, AB = 4cm,AA' = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ ABC.A'B'C' ?
Xét tam giác ABC có nửa chu vi của tam giác là:
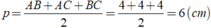
Khi đó ta có
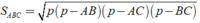

+ Diện tích xung quanh của hình lăng trụ

Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AB = 3 cm, AC = 4 cm, BC' =13 cm. Hãy tính:
a) Diện tích xung quanh lăng trụ;
b) Thể tích hình lăng trụ
Bài 1 : Cho hình lăng trụ đứng ABC.PQR có đáy là tam giác ABC vuông tại A. Cho biết AB = 5cm, AC =12cm, AP = 10cm.
a) Vẽhình và cho biết số cạnh và số đỉnh của lăng trụ.
b)Tính thể tích của lăng trụ.
c)Tính diện tích xung quanh, diện tích toàn phần của lăng trụ.
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều, M là trung điểm của BC, AA’ = AM = a. Thể tích của lăng trụ bằng:
A. a 2 3 3
B. a 3 3 3
C. a 2 2 2
D. a 3 3 9
Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông, AB=BC=a, cạnh bên \(AA'=a\sqrt{2}\). Gọi M là trung điểm cạnh BC. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa 2 đường thẳng AM, B'C
Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)
Bài 1 : Cho hình lăng trụ đứng ABC.PQR có đáy là tam giác ABC vuông tại A. Cho biết AB = 5cm, AC =12cm, AP = 10cm.
a)Vẽ hình và cho biết số cạnh và số đỉnh của lăng trụ.
b)Tính thể tích của lăng trụ.
c)Tính diện tích xung quanh, diện tích toàn phần của lăng trụ.
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, AA'= 3 a 2 Biết rằng hình chiếu vuông góc của A' lên (ABC) là trung điểm BC. Tính thể tích V của lăng trụ đó.
A. V = 2 a 3 3
B. V = 3 a 3 4 2
C. V = a 3 3 2
D. V = a 3