Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và B A D ^ = B A A ' ^ = D A A ' ^ = 60 ° . Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
A. a 5 5
B. a 6 3
C. a 10 5
D. a 3 3
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc tại đỉnh B đều bằng 60 o .
Đường thẳng B’C vuông góc với đường thẳng:
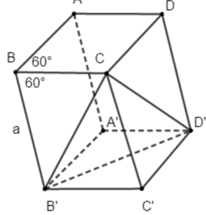
A. AC
B. CD
C. BD
D. A’A
Phương án A sai vì tam giác ACB’ có ba cạnh bằng a
Phương án C sai vì tam giác CB’D’ có ba cạnh a, a√3,a√3 nên không thể vuông tại B’
Phương án D sai vì góc giữa đường thẳng B’C và AA’ bằng 0 o
Phương án B đúng vì:
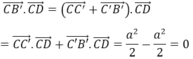
Đáp án B
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc tại đỉnh B đều bằng 60 o .
Cặp đường thẳng nào sau đây không vuông góc với nhau?
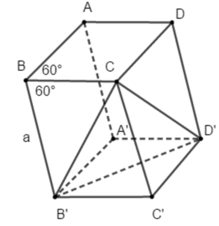
A. B’C và AD’
B. BC’ và A’D
C. B’C và CD’
D. AC và B’D’
Phương án A, B và D đều sai
Phương án C đúng vì tam giác CB’D’ có ba cạnh bằng a, a√3,a√3 nên không thể vuông tại B’
Đáp án C
Cho hình hộp đứng ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a, A B C ^ = 45 ° . Tính thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = a 3 2 4
B. V = a 3
C. V = a 3 2 2
D. V = 2 a 3
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh , BD = 3a, hình chiếu vuông góc của B lên mặt phẳng (A’B’C’D’) là trung điểm của A’C’. biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD’C’) bằng 21 7 . Tính theo a thể tích khối hộp ABCD.A’B’C’D’
A. 9 a 3 4
B. a 3
C. 9 a 3 2
D. 3 a 3 2
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng 2 2 a 3 đáy ABCD là hình thoi cạnh a và B A D ^ = 45 ° . Khoảng cách giữa hai đáy ABCD và A’B’C’D’ của hình hộp bằng
A. 4a
B. 2a
C. 2 2 a
D. 4 2 a
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD = 120 0 và AA' = 7 a 2 . Hình chiếu vuông góc của A’ lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
![]()
![]()
![]()
![]()
Chọn đáp án B
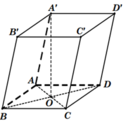
Gọi O = AC ∩ BD.Từ giả thiết suy ra A'O ⊥ ABCD
Cũng từ giả thiết, suy ra ABC là tam giác đều nên
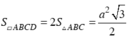
Đường cao khối hộp
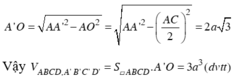
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, B C D ^ = 120 ° và A A ' = 7 a 2 Hình chiếu vuông góc của A lên mặt phẳng ABCD trùng với giao điểm của AC và BD.Tính theo a thể tích khối hộp ABCD.A’B’C’D’:
A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , BD=3a. Hình chiếu vuông góc của B trên mặt phẳng (A'B'C'D') trùng với trung điểm A’C’. Gọi α là góc giữa 2 mặt phẳng (ABCD) và (CDD'C'). Thể tích của khối hộp ABCD.A'B'C'D' bằng
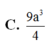
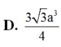
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD ^ = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3