Cho hình chóp tứ giác đều S.BACD có cạnh đáy bằng a. Các điểm M; N; P lần lượt là trung điểm của SA; SB; SC. Mặt phẳng (MNP) cắt hình chóp theo 1 thiết diện có diện tích bằng?
A. a 2
B. a 2 2
C. a 2 4
D. a 2 8
Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông tâm O các cạnh bên và các cạnh đáy đều bằng a Gọi M là trung điểm SC .Góc giữa 2 mặt phẳng MBD và ABCD bằng bao nhiêu?
Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và có thể tích V = a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy.
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Đáp án là C.
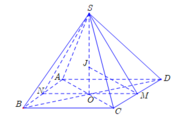
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO
V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .
Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a
Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.
Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .
Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng 60 o Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
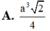
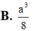
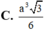
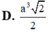
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a góc giữa mặt bên và mặt đáy bằng 60 ° . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD,DC. Thể tích khối tứ diện ACMN là
A. a 3 2 4
B. a 3 8
C. a 3 3 6
D. a 3 2 2
Đáp án C
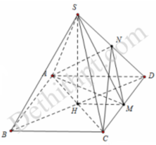
Ta có S C D ; A B C ^ = S M H ^ = 60 °
Khi đó S H = H M tan 60 ° = a 3
Mặt khác
S A C M = 1 2 A D . C M = 1 2 2 a . a = a 2
d N ; A C M = 1 2 S H = a 3 2 ⇒ V N . A C M = 1 3 d N ; A C M = a 3 3 6
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 o . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là:
A. a 3 2 4
B. a 3 8
C. a 3 3 6
D. a 3 2 2
Chọn C
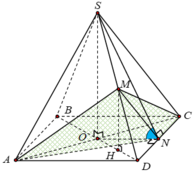
Gọi O là tâm của hình vuông ABCD.
Góc giữa cạnh bên (SAB) và mặt đáy là góc S N O ^ = 60 o
Xét tam giác SNO, ta có SO = NO tan600 = a 3
Lại có M là trung điểm của SD nên:
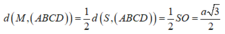
N là trung điểm của CD nên S ∆ A C N = 1 4 S A B C D = 1 4 4 a 2 = a 2
Do đó, thể tích khối MACN là
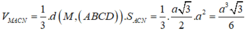
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 o . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
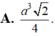
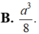
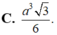
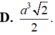
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 0 . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là
A. a 3 2 4 .
B. a 3 8 .
C. a 3 3 6 .
Đáp án C

Góc giữa mặt bên và mặt đáy bằng 60 0
⇒ S N O ^ = 60 0 ⇒ S O = N O . tan 60 0 = a 3
Kẻ MH song song với S O ⇒ M H = 1 2 S O = a 3 2 và M H ⊥ A N C
Ta có: d t A N C = 1 2 A D . N C = 1 2 2 a . a = a 2
⇒ V A M N C = 1 3 M H . d t A N C = 1 3 a 3 2 . a 2 = a 3 3 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 ° Gọi M, N lần lượt là trung điểm của các cạnh SD, DC. Thể tích khối tứ diện ACMN là
A. a 3 8 .
B. a 3 2 2 .
C. a 3 3 6 .
D. a 3 2 4 .