Trong mp Oxy, cho đường thẳng (d): 2018x + 2019y – 1 =0 và vectơ u → 2019 ; m . Tìm m để phép tịnh tiến theo vectơ u → biến (d) thành chính nó
A.–2018
B. –2019
C. 2018
D. 2019
Trong mp Oxy, cho đường thẳng (d): 2018x + 2019y – 1 =0 và vectơ u → 0 ; m . Tìm m để phép tịnh tiến theo vectơ u → biến (d) thành chính nó
A. 0
B. 1
C. 2
D. 3
Đáp án A
Phép tịnh tiến biến(d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương v → của (d) : v → ( 2019 ; − 2018 ) = k u → = 0 ; k m =>m = 0
=>có một giá trị m = 0 để biến (d) thành chính nó
Trong mp Oxy, cho đường thẳng (d): 2018x + 2019y – 1 = 0 và vectơ u → 2 ; m . có bao nhiêu giá trị của m để phép tịnh tiến theo vectơ u → biến (d) thành chính nó
A.0
B.1
C.2
D.3
Đáp án B
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → 2 k ; k m =>k 2019 2 => m = − 4046 2019
=>có một giá trị m = − 4046 2019 để biến (d) thành chính nó
Trong mp Oxy, cho d: x – 3y + 1 = 0. Để phép tịnh tiến theo vectơ u → biến d thành chính nó thì u → phải là vectơ nào trong các vectơ dưới đây?
A. (3;1)
B. (1;–3)
C. (–1;3)
D. (–3;–1)
Đáp án D
Để biến d thành chính nó, ta tịnh tiến d theo VTCP của nó.
Cho \(2018x^3=2019y^3=2020z^3\) và \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=8\)
Tính giá trị biểu thức: \(B=\frac{\sqrt[3]{2018x^2+2019y^2+2020z^2}}{\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020}}\)
Lời giải:
Đặt mẫu số của $B$ là $M$.
Từ \(2018x^3=2019y^3=2020z^3\)
\(\Rightarrow \sqrt[3]{2018}x=\sqrt[3]{2019}y=\sqrt[3]{2020}z=\frac{\sqrt[3]{2018}}{\frac{1}{x}}=\frac{\sqrt[3]{2019}}{\frac{1}{y}}=\frac{\sqrt[3]{2020}}{\frac{1}{z}}=\frac{\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\)
\(=\frac{\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020}}{8}=\frac{M}{8}\)
\(\Rightarrow \left\{\begin{matrix} x=\frac{M}{8\sqrt[3]{2018}}\\ y=\frac{M}{8\sqrt[3]{2019}}\\ z=\frac{M}{8\sqrt[3]{2020}}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} 2018x^2=\frac{\sqrt[3]{2018}M^2}{64}\\ 2019y^2=\frac{\sqrt[3]{2019}M^2}{64}\\ 2020z^2=\frac{\sqrt[3]{2020}M^2}{64}\end{matrix}\right.\)
\(\Rightarrow 2018x^2+2019y^2+2020z^2=\frac{M^2(\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020})}{64}=\frac{M^3}{64}\)
\(\Rightarrow B=\frac{\sqrt[3]{\frac{M^3}{64}}}{M}=\frac{M}{4M}=\frac{1}{4}\)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+y-4z=0, đường thẳng d : x - 1 2 = y + 1 - 1 = z - 3 1 và điểm A(1;3;1) thuộc mặt phẳng (P). Gọi ∆ là đường thẳng đi qua A, nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi u → = a ; b ; 1 là một vectơ chỉ phương của đường thẳng ∆. Tính a+2b.
A. 7
B. -3
C. 0
D. 4
trong mặt phẳng oxy, cho đường tròn (C):\(x^2+y^2-8x+6y+ 21=0\) và đường thẳng d: \(x+ y-1=0\)
Hai tiếp tuyến của đường tròn C tại A,B vuông góc với nhau tại điểm N. Biết N thuộc đường thẳng d. Tìm toạ độ điểm N
Trong mặt phẳng với hệ trục tọa đô Oxy , cho hai đường thẳng ∆1: x- y+ 1= 0 và ∆2: 2x + y-1 = 0 và điểm P (2;1) .Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng ∆1, ∆2 lần lượt tại hai điểm A: B sao cho P là trung điểm AB?
A. 4x – y- 7 = 0
B. x+ 4y- 4= 0
C. x- 4y-7= 0
D . 2x + y- 7= 0
Đáp án A
Ta có 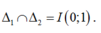
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
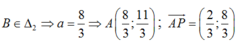
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0
4. Trong mp toạ độ Oxy cho đg thẳng d có pt 2x - y +1=0 . Để phép tịnh tiến theo vectơ v biến d thành chính nó thì vectơ v phải lad vectơ nào?
5. Trong mp toạ độ Oxy , ảnh của đg tròn (x -2)^2 + (y -1)^2=16. Qua phép tịnh tiến theo vectơ v= (1;3) là đg tròn có pt?
4.
Để phép tịnh tiến theo \(\overrightarrow{v}\) biến d thành chính nó thì \(\overrightarrow{v}\) phải là 1 vecto chỉ phương của d
Khi đó \(\overrightarrow{v}=k\left(1;2\right)\) với k là số thực
5.
Đường tròn tâm \(I\left(2;1\right)\) bán kính \(R=4\)
Phép tịnh tiến theo \(\overrightarrow{v}\) biến đường tròn thành đường tròn tâm I' bán kính R=4
\(I'=T_{\overrightarrow{v}}\left(I\right)\Rightarrow\left\{{}\begin{matrix}x_{I'}=2+1=3\\y_{I'}=3+1=4\end{matrix}\right.\) \(\Rightarrow I'\left(3;4\right)\)
Phương trình đường tròn: \(\left(x-3\right)^2+\left(y-4\right)^2=16\)
Trong mp Oxy, cho đường tròn C : x 2 + y 2 − 4 y − 21 = 0 . Ảnh (C’) của (C) qua phép tịnh tiến theo vectơ u → = 2 ; − 2 là
A. ( x − 2 ) 2 + y 2 = 5
B. x 2 + y − 2 2 = 25
C. x − 2 2 + y 2 = 25
D. x 2 + y − 2 2 = 5
Đáp án C
(C) có tâm I(0;2), bán kính 5
Tịnh tiến theo vectơ u → biến I thành I’(2; 0)
=>Phương trình đường tròn (C’): ( x − 2 ) 2 + y 2 = 25