Cho hai đường thẳng d 1 : x = 1 + 2 t y = 2 + 3 t z = 3 + 4 t và d 2 : x = 3 + 4 t y = 5 + 6 t z = 7 + 8 t
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d 1 ⊥ d 2 .
B. d 1 / / d 2 .
C. d 1 ≡ d 2 .
D. d 1 v à d 2 chéo nhau
Những câu hỏi liên quan
Cho đường thẳng d: y = (m − 1)x + mvà d′: y = ( m 2 − 1)x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau
A. m = 0 và m = 3
B. m = 0 và m = 2
C. m = 0 và m = 1
D. m = 0 và m = 4
Cho đường thẳng
Δ
:
x
+
1
2
y
3
x
+
1
−
1
và hai điểm
A
1
;
2
;
−
1
,
...
Đọc tiếp
Cho đường thẳng Δ : x + 1 2 = y 3 = x + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:
A. x − 3 2 = y 2 = z + 5 − 1
B. x − 1 = y + 2 3 = z 4
C. x + 2 3 = y 1 = z − 1 − 1
D. x − 1 1 = y − 2 2 = z + 1 − 1
Đáp án là D.
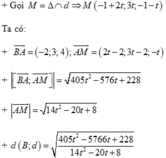
Xét f t = 405 t 2 − 576 t + 228 14 t 2 − 20 t + 8 ⇒ f ' t = − 36 t 2 + 96 t − 48 14 t 2 − 20 t + 8 2
f ' t = 0 ⇔ t = 2 t = 2 3 . Vậy max f t = f 2 ⇒ t = 2
+ Đường thẳng d đi qua A 1 ; 2 ; − 1 và có VTCP A M → = 2 ; 4 ; − 2 = 2 1 ; 2 ; − 1
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d
1
:
x
-
1
2
y
-
1
-
1
z
+
1
1
,
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Chọn A
Vì A thuộc 
nên A (1+2t;1-t;-1+t).
Vì B thuộc 
nên B (-2+3t';-1+t';2+2t').
Thay vào (3) ta được t=1, t'=2 thỏa mãn.
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho hai đường thẳng d và d’ có phương trình lần lượt là
x
-
2
2
y
+
4
3
1
-
z
2
;
x
4...
Đọc tiếp
Trong không gian Oxyz cho hai đường thẳng d và d’ có phương trình lần lượt là x - 2 2 = y + 4 3 = 1 - z 2 ; x = 4 t y = - 1 + 6 t z = - 1 + 4 t . Xác định vị trí tương đối của hai đường thẳng d và d’.
A. Song song nhau
B. Trùng nhau
C. Cắt nhau
D. Chéo nhau
Đường thẳng d qua M ( 2;-4;1 ) và có vectơ chỉ phương là u → 2 ; 3 ; 2
Đường thẳng d’ qua M' ( 0;1;-1 ) và có vectơ chỉ phương là u ' → = 4 ; 6 ; 4
Do u → và u ' → cùng phương đồng thời M ∉ d ' nên hai đường thẳng đó song song nhau.
Đáp án A
Đúng 0
Bình luận (0)
Cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai...
Đọc tiếp
Cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1;2;-1), B(3;-1;-5) . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Phương trình của d là:
A. x - 3 2 = y 2 = z + 5 - 1
B. x - 1 = y + 2 3 = z 4
C. x + 2 3 = y 1 = z - 1 - 1
D. x - 1 1 = y - 2 2 = z + 1 - 1
Đáp án là D.
Ta có:
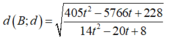
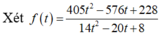
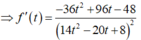
Đường thẳng d đi qua A(1;2;-1) và có VTCP
Đúng 0
Bình luận (0)
Cho hai đường thẳng (d): x+2y-1=0 và d’: x-3y+2=0.Số đo góc giữa hai đường thẳng là:
A,600
B,900
C,69034''
D,450
cos(d,d')=\(\dfrac{\left|1.1+2.\left(-3\right)\right|}{\sqrt{1^2+2^2}.\sqrt{1^2+\left(-3\right)^2}}\)= \(\dfrac{\sqrt{2}}{2}\)=450
Đúng 0
Bình luận (0)
Cho hai đường thẳng :
(d 1 ) : y = - 3x + m + 1
(d 2 ) : y = ( 2k + 6 ) x + 2 – m ( k ≠ - 3 )
a) Xác định k, m để hai đường thẳng trùng nhau
b) Xác định k, m để hai đường thẳng song song
c) Xác định k, m để hai đường thẳng cắt nhau
d) Xác định k, m để hai đường thẳng vuông góc với nhau
Để 2 đường thẳng trùng nhau \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m=m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m=\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng song song \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m\ne m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m\ne\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng cắt nhau \(\Rightarrow2k+6\ne-3\Rightarrow k\ne-\frac{9}{2}\)
Để 2 đường thẳng vuông góc \(\Rightarrow\left(2k+6\right).\left(-3\right)=1\Rightarrow k=-\frac{19}{6}\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
:
x
+
1
2
y
3
z
+
1
-
1
và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
A . x - 3 2 = y 2 = z + 5 - 1
B . x - 1 = y + 2 3 = z 4
C . x + 2 3 = y 1 = z - 1 - 1
D. Tất cả sai
Chọn D
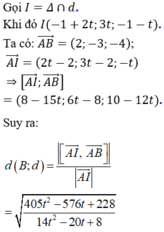
Xét hàm số:
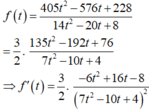
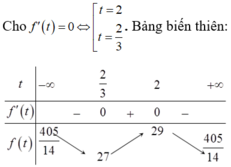
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra 
. Chọn một vectơ chỉ phương của đường thẳng d là 
Vậy phương trình đường thẳng 
Đúng 0
Bình luận (0)
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Có bao nhiêu giá trị của m để hai đường thẳng d; d’ song song với nhau.
A. 0
B. 1
C. 2
D. 3
Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
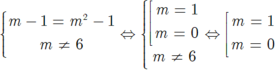
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
d
:
x
1
+
t
y
2
-
t
z...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
