Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
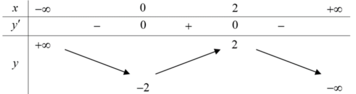
A. y = x3 – 3x2 – 1
B. y = -x3 + 3x2 – 2
C. y = -x3 + 3x2 – 1
D. y = -x3 – 3x – 2
Cho hàm số y = - x 3 - 3 x 2 + 9 x + 1 xác định trên R. Bảng biến thiên của hàm số là bảng nào trong các bảng biến thiên dưới đây?
A. 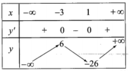
B. 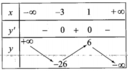
C. 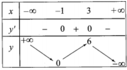
D. 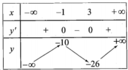
Cho hàm số y = x 3 + 3 x 2 − 4 có bảng biến thiên sau, tìm a và b:
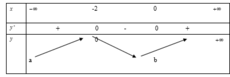
A. a = + ∞ ; b = 2
B. a = − ∞ ; b = − 4
C. a = − ∞ ; b = 1
D. a = + ∞ ; b = 3
Chọn B.
Phương pháp:
Tính giới hạn của hàm số khi x tiến đến âm vô cùng để tìm a và tính giá trị của hàm số tại x = 0 để tìm b.
Cách giải:
![]()
Cho hàm số y = x 3 + 3 x 2 - 4 có bảng biến thiên sau, tìm a và b:
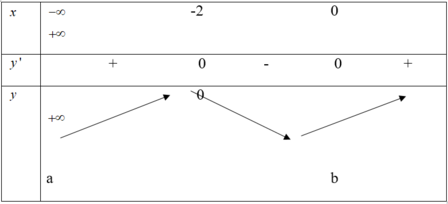
A. a = + ∞ ; b = 2
B. a = - ∞ ; b = - 4
C. a = - ∞ ; b = 1
D. a = + ∞ ; b = 3
khảo sát sự biến thiên và vẽ đồ thị hàm số:
a. y=x3-3x2+2
b. y=x3+1
Cho hàm số f ( x ) = x 3 - 3 x 2 + 5 x + 1 Hàm số y=g(x) có bảng biến thiên như sau
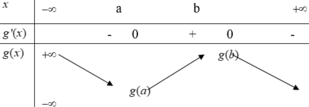
Biết rằng a , b ∈ R và a<b;g(a).g(b)<0 Phương trình g(f(x))=0 có tất cả bao nhiêu nghiệm thực?
A. 3
B. 9
C. 5
D. 1
Vì 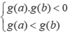
![]() Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ
Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ ![]() Vì vậy g(f(x)0
Vì vậy g(f(x)0 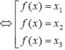
Hàm số f(x) có ![]() đồng biến trên R do đó mỗi phương trình
đồng biến trên R do đó mỗi phương trình ![]() có một nghiệm thực duy nhất.
có một nghiệm thực duy nhất.
Vậy phương trình đã cho có 3 nghiệm thực.
Chọn đáp án A.
Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x 3 + 3 x 2 + 1

+ Bảng biến thiên:
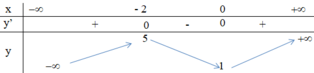
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
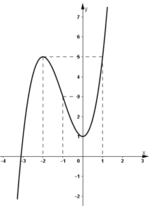
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
Hàm số y = - x 3 - 3 x 2 + 2 nghịch biến khi x thuộc khoảng nào sau đây?
![]()
![]()
![]()
![]()
Hàm số y = x 3 + 3 x 2 nghịch biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()
Hàm số y = x 3 + 3 x 2 − 4 nghịch biến trên khoảng nào sau đây?
A. ℝ .
B. ( − ∞ ; − 2 ) .
C. ( 0 ; + ∞ ) .
D. ( − 2 ; 0 ) .
Hàm số y = x 3 + 3 x 2 - 4 nghịch biến trên khoảng nào sau đây?
A. - ∞ ; - 2
B. 0 ; + ∞
C. - 2 ; 0
D. R