Tổng tất cả các nghiệm thuộc khoảng 0 ; 11 π của phương trình 4 sin 3 x + sin 5 x − 2 sin x . cos 2 x = 0 là
A. 328 π
B. 176 π
C. 209 π
D. 352 π
Tính tổng hợp tất cả các nghiệm thuộc khoảng 0 ; π của phương trình: 2 cos 3 x = sin x + cos x
A. π
B. 3 π
C. 3 π 2
D. π 2
Cho phương trình m x 2 + 4 π 2 - 4 π 2 cos x . Tổng tất cả các giá trị nguyên của tham số m để phương trình có nghiệm thuộc khoảng 0 ; π 2 bằng
A. -54
B. 35
C. -35
D. 51
Tính tổng tất cả các nghiệm thuộc khoảng 0 ; 2 π của phương trình 2 c os 3 x = sin x + cos x .
A. 6 π
B. 11 π 2
C. 8 π
D. 9 π 2
Tính tổng tất cả các nghiệm thuộc khoảng 0 ; 2 π của phương trình 2 cos3x = sinx + cosx.
A. 6 π
B. 11 π 2
C. 8 π
D. 9 π 2
Tính tổng tất cả các nghiệm thuộc khoảng 0 ; 2 π của phương trình 2 cos 3 x = sin x + cos x
A. 6 π
B. 11 π 2
C. 8 π
D. 9 π 2
Tính tổng tất cả các nghiệm của phương trình cos 5 x cos x = cos 4 x cos 2 x + 3 cos 2 x + 1 thuộc khoảng - π ; π
![]()
![]()
![]()
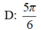
Biết S=(a;b) là tất cả các giá trị thực của m để phương trình
cos
3
x
-
cos
2
x
+
m
cos
x
-
1
=
0
có đúng 8 nghiệm thực phân biệt thuộc khoảng 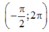 . Tính tổng T=a+b
. Tính tổng T=a+b
A. 4
B. -2
C. 17 4
D. 25 4
Đáp án D
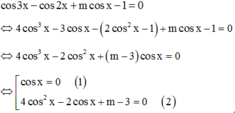
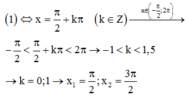
→
(1) có 2 nghiệm thuộc 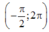
Để phương trình có đúng 8 nghiệm thuộc khoảng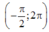 thì (2) phải có đúng 6 nghiệm phân biệt thuộc
thì (2) phải có đúng 6 nghiệm phân biệt thuộc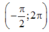 và khác
x
1
;
x
2
và khác
x
1
;
x
2
Đặt t = cos x ( - 1 ≤ x ≤ 1 ) , (2) trở thành f ( t ) = 4 t 2 - 2 t + m - 3 = 0 ( 3 )
+ Nếu
0
<
t
<
1
thì phương trình cosx=t có 3 nghiệm phân biệt thuộc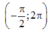
+ Nếu
-
1
<
t
<
0
thì phương trình cosx=t có 2 nghiệm phân biệt thuộc khoảng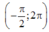
Do đó (2) có đúng 6 nghiệm phân biệt thuộc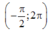
⇔ (3) có 2 nghiệm t 1 ; t 2 thỏa mãn 0 < t 1 < t 2 < 1
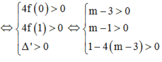

Biết S= (a;b) là tập tất cả các giá trị thực của m để phương trình cos3x - cos2x+ mcosx-1 = 0 có đúng 8 nghiệm thực phân biệt thuộc khoảng - π 2 ; 2 π .Tính tổng T = a+b.
A. 4..
B. -2
C. 17 4
D. 25 4
tổng tất cả các nghiệm thuộc [0; 2π] của phương trình 2sinx - \(\sqrt{3}\) = 0 là ?
\(2sinx-\sqrt{3}=0\)
\(\Leftrightarrow sinx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(0\le\dfrac{\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{6}\le k\le\dfrac{5}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{\pi}{3}\)
\(0\le\dfrac{2\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{3}\le k\le\dfrac{4}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{2\pi}{3}\)
\(\Rightarrow x_1+x_2=\pi\)