xét tam giác ADC và tam giác BAC có

góc C=góc C,AC/BC=DC/AC=2/3

=> tam giác ADC đồng dạng tam giác BAC (c-g-c)

=> AD/AB=AC/BC=> AD=AB.AC/BC=12.18/27=8cm

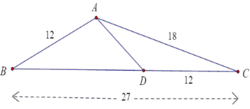
Ta có

A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A

Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)

Nên ΔACB ~ ΔDCA (c.g.c)

⇒ A C D C = A B D A ⇔ 3 2 = 12 D A ⇒ D A   = 2.12 3 =   8 c m

Đáp án: D

Tự vẽ hình nhá!

Ta có:

\(\dfrac{AC}{BC}=\dfrac{18}{27}=\dfrac{2}{3}\)

\(\dfrac{CD}{AC}=\dfrac{12}{18}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CD}{AC}\)

Xét \(\Delta ADC\) và \(\Delta BAC\) có:

Góc C chung

\(\dfrac{AC}{BC}=\dfrac{CD}{AC}\)( cmt)

Do đó: \(\Delta ADC\sim\Delta BAC\) (c.g.c)

=> \(\dfrac{AD}{AB}=\dfrac{AC}{BC}\Rightarrow AD=\dfrac{AB.AC}{BC}=\dfrac{12.18}{27}=8\)

Vậy AD = 8(cm)

C

C

C nha 

a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)

\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm

b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)

\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm

Giúp Mình Nhé

tk rồi mình giúp nhé

a) Vì AB=AC nên tam giác ABC cân tại A 
Mà AH \(⊥\)BC => AH vừa là đường cao ,đường trung trực, vừa là đường phân giác => góc BAH = góc CAH
Xét hai tam giác vuông ABH và ACH có 
góc H chung
AB=AC(gt) 
góc HAB  = góc HAC (cmt)
Vậy : tam giác ABH= tam giác ACH (g-c-g) (đpcm)
b) M là trung điểm BH => MH=BM (1)
Lại có MA=MD (gt) (2)
Từ (1) và (2) => ABDH là hình bình hành ( haiđường chéo cắt nhau tại trung điểm mỗi đường)
=> AH // BD
Mà AH \(⊥\)BC (gt) 
Nên BD \(⊥\)BC (đpcm)
c) AH là đường trung trực (cmt) => BH=HC=BC/2=18/2=9(cm)
Xét tam giác vuông AHB có:
\(AB^2=AH^2+BH^2\Rightarrow AH^2=AB^2-BH^2=15^2-9^2=225-81=144\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)