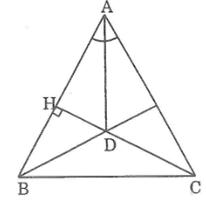
Cho tam giác ABC cân tại A, B ^ = 65 0 , đường cao CH = 3,6. Hãy giải tam giác ABC
A. A ^ = 50 0 ; C ^ = 65 0 ; AB = AC = 5,6; BC = 8,52
B. A ^ = 50 0 ; C ^ = 65 0 ; AB = AC = 5,6; BC = 4,42
C. A ^ = 50 0 ; C ^ = 65 0 ; AB = AC = 4,7; BC = 4,24
D. A ^ = 50 0 ; C ^ = 65 0 ; AB = AC = 4,7; BC = 3,97